同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).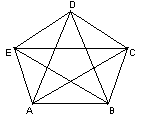
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
真真、明明、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知真真已握了5次手,明明已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
已知,如图,点D在边BC上,点E在△ABC外部,DE交AC于F,若AD=AB,∠1=∠2=∠3.求证:BC=DE.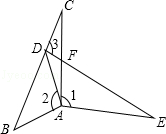
如图,在△MNP中,∠MNP=45°,H是高MQ和高NR的交点,求证:HN=PM.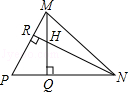
小亮家距离学校8千米,昨天早晨,小亮骑车上学途中,自行车“爆胎”,恰好路边有“自行车”维修部,几分钟后车修好了,为了不迟到,他加快了骑车到校的速度.回校后,小亮根据这段经历画出如下图象.该图象描绘了小亮行的路程S与他所用的时间t之间的关系.请根据图象,解答下列问题: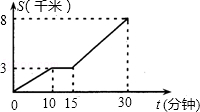
(1)小亮行了多少千米时,自行车“爆胎”?修车用了几分钟?
(2)小亮到校路上共用了多少时间?
(3)如果自行车没有“爆胎”,一直用修车前的速度行驶,那么他比实际情况早到或晚到学校多少分钟(精确到0.1)?
先化简,再求值:2x2+(﹣x2+3xy+2y2)﹣(x2﹣xy+2y2),其中x= ,y=3.
,y=3.
某位同学做一道题:已知两个多项式A、B,求A﹣B的值.他误将A﹣B看成A+B,求得结果为3x2﹣3x+5,已知B=x2﹣x﹣1.(1)求多项式A;(2)求A﹣B的正确答案.