如图,直三棱柱 中,
中, 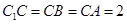 ,
,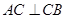 .
. 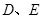 分别为棱
分别为棱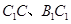 的中点.
的中点.
(1)求二面角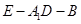 的平面角的余弦值;
的平面角的余弦值;
(2)在线段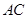 上是否存在一点
上是否存在一点 ,使得
,使得 平
平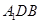 ?
?
若存在,确定其位置;若不存在,说明理由.
已知函数 在
在 内有极值.
内有极值.
(Ⅰ)求实数的取值范围;
(Ⅱ)若 ,
,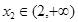 ,且
,且 时,求证:
时,求证:
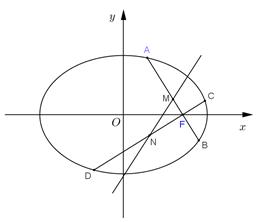
已知椭圆 的右焦点
的右焦点 ,离心率为
,离心率为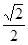 ,过
,过 作两条互相垂直的弦
作两条互相垂直的弦 ,设
,设 的中点分别为
的中点分别为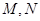 .
.
(1)求椭圆的方程;
(2)证明:直线 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3)若弦 的斜率均存在,求
的斜率均存在,求 面积的最大值.
面积的最大值.
下图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人
(Ⅰ)求该专业毕业总人数N和90~95分数段内的人数 ;
;
(Ⅱ)现欲将90~95分数段内的 名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为
名毕业生分配往甲、乙、丙三所学校,若向学校甲分配两名毕业生,且其中至少有一名男生的概率为 ,求
,求 名毕业生中男女各几人(男女人数均至少两人)?
名毕业生中男女各几人(男女人数均至少两人)?
(Ⅲ)在(Ⅱ)的结论下,设随机变量 表示n名毕业生中分配往乙学校的三名学生中男生的人数,求
表示n名毕业生中分配往乙学校的三名学生中男生的人数,求 的分布列和数学期望.
的分布列和数学期望.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD
⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
(Ⅰ)求证:EF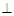 平面PAD;
平面PAD;
(Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小;
已知锐角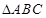 的三个内角
的三个内角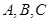 所对的边分别为
所对的边分别为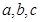 .且
.且 。
。
(1)求角 的大小;
的大小;
(2)求 的取值范围.
的取值范围.