已知椭圆 的右焦点
的右焦点 ,离心率为
,离心率为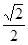 ,过
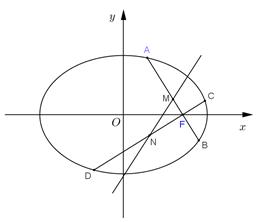
,过 作两条互相垂直的弦
作两条互相垂直的弦 ,设
,设 的中点分别为
的中点分别为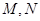 .
.
(1)求椭圆的方程;
(2)证明:直线 必过定点,并求出此定点坐标;
必过定点,并求出此定点坐标;
(3)若弦 的斜率均存在,求
的斜率均存在,求 面积的最大值.
面积的最大值.
已知函数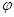 (x)=
(x)=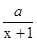 ,a是正常数。(1)若f(x)=
,a是正常数。(1)若f(x)= 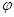 (x)+lnx,且a=
(x)+lnx,且a=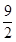 ,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+
,求函数f(x)的单调递增区间;(2)若g(x)=∣lnx∣+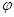 (x),且对任意的x
(x),且对任意的x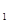 ,x
,x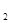 ∈(0,2〕,且x
∈(0,2〕,且x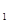 ≠x
≠x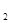 ,都有
,都有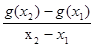 <-1,求a的取值范围
<-1,求a的取值范围
在某次测验中,有6位同学的平均成绩为75分.用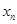 表示编号为
表示编号为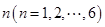 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
成绩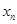 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学成绩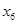 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差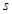 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间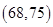 中的概率.
中的概率.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。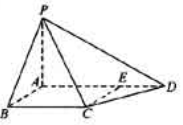
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
在△ABC中,内角A,B,C的对边分别为a,b,c.已知 .
.
(1)求 的值;
的值;
(2)若cosB= ,△
,△
(本小题满分10分)
已知:

通过观察上述两等式的规律,请你写出一般性的命题,并证明你的结论