某仪器用电场和磁场来控制电子在材料表面上方的运动，如图所示，材料表面上方矩形区域PP′N′N充满竖直向下的匀强电场，电场宽为d；矩形区域NN′M′M充满垂直纸面向里的匀强磁场，磁感应强度为B，长为3s，宽为s；NN′为磁场与电场之间的薄隔离层。一个电荷量为e、质量为m、初速为零的电子，从P点开始被电场加速经隔离层垂直进入磁场，电子每次穿越隔离层，时间极短、运动方向不变，其动能损失是每次穿越前动能的10%，最后电子仅能从磁场边界M′N′飞出。不计电子所受重力。
（1）控制电子在材料表面上方运动，最大的电场强度为多少？
（2）若电子以上述最大电场加速，经多长时间将第三次穿越隔离层？
（3）A是M′N′的中点，若要使电子在A、M′间垂直于AM′飞出，求电子在磁场区域中运动的时间。
现代家庭电器化程度越来越高，用电安全是一个十分突出的问题。
下表提供了一组部分人的人体电阻平均值数据。
| 测量项目 |
完全干燥时 |
出汗或潮湿时 |
||
| 电阻 |
电流（加220V） |
电阻 |
电流（加220V） |
|
| 手与手之间 |
200kΩ |
1.1×10-3A |
5kΩ |
|
| 手与脚之间 |
300kΩ |
7.3×10-4A |
8kΩ |
|
| 手与塑料鞋底之间 |
8000kΩ |
2.8×10-5A |
10kΩ |
①从表中可看出干燥时手与手之间电阻大约是潮湿时手与手之间电阻的倍。
②在空格中填入，对人体加220伏电压后的电流值。
③若对人的安全电流是25mA以下，上述哪几项是十分危险的。
④电路上有规格为10A的熔丝（俗称保险丝），如右图所示用电器R的功率是1500W，这时通过熔丝实际电流是多少？一个潮湿的人，手脚触电，为什么熔丝不会断（即熔丝不能救人命）。
如400W）每天平均工作1h。这些用电器一个月的耗电量是多少？若每kw.h电费为0.6元，每果家里的电视机（100W）、和洗衣机（月应缴多少电费？（每月按30天算）。
如图所示，在光滑的水平面上，停着质量为
、长为L的小车，一个质量为
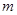的滑块从车内底板的正中央获得大小为
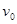的速度后向车壁运动，若滑块与车底板之间的动摩擦因数为
，滑块与车壁之间的碰撞没有能量损失，求滑块与车壁的碰撞次数。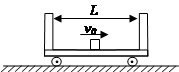
如图所示，质量为m的砝码A放置在质量为M的滑块B上，B与弹簧相连，它们一起在光滑的水平面上作简谐运动，弹簧的劲度系数为k，砝码与滑块之间的动摩擦因数为
，要使砝码与滑块在振动过程中不发生相对运动，问最大振幅等于多少？（设最大静摩擦力等于滑动摩擦力）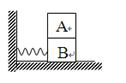
风力发电作为新型环保新能源，近几年来得到了快速发展，如图所示风车阵中发电机输出功率为100kW，输出电压是250V，用户需要的电压是220V，输电线电阻为10Ω.若输电线因发热而损失的功率为输送功率的4%，试求：
（1）在输电线路中设置的升、降压变压器原、副线圈的匝数比．
（2）用户得到的电功率是多少．