如图所示,质量为m的砝码A放置在质量为M的滑块B上,B与弹簧相连,它们一起在光滑的水平面上作简谐运动,弹簧的劲度系数为k,砝码与滑块之间的动摩擦因数为 ,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)
,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)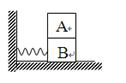
严重的雾霾天气,对国计民生已造成了严重的影响,汽车尾气是形成雾霾的重要污染源,"铁腕治污"已成为国家的工作重点,地铁列车可实现零排放,大力发展地铁,可以大大减少燃油公交车的使用,减少汽车尾气排放。若一地铁列车从甲站由静止启动后做直线运动,先匀加速运动20s达到最高速度72 / ,再匀速运动80 ,接着匀减速运动15 到达乙站停住。设列车在匀加速运动阶段牵引力为1×106 ,匀速阶段牵引力的功率为6×103 ,忽略匀减速运动阶段牵引力所做的功。

(1)求甲站到乙站的距离;
(2)如果燃油公交车运行中做的功与该列车从甲站到乙站牵引力做的功相同,求公交车排放气体污染物的质量。(燃油公交车每做1焦耳功排放气体污染物3×10-6克)
如图,在场强大小为 、水平向右的匀强电场中,一轻杆可绕固定转轴 在竖直平面内自由转动。杆的两端分别固定两电荷量均为 的小球 、 ; 带正电, 带负电; 、 两球到转轴 的距离分别为 、 ,所受重力大小均为电场力大小的 倍,开始时杆与电场夹角为 ( )。将杆从初始位置由静止释放,以 点为重力势能和电势能零点。求:
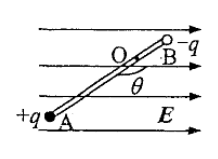
(1)初始状态的电势能 ;
(2)杆在平衡位置时与电场间的夹角 ;
(3)杆在电势能为零处的角速度 。
如图(a)两相距 的平行金属导轨固定于水平面上,导轨左端与阻值 的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场,质量 的金属杆垂直于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略,杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v-t图像如图(b)所示,在 时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0,求:
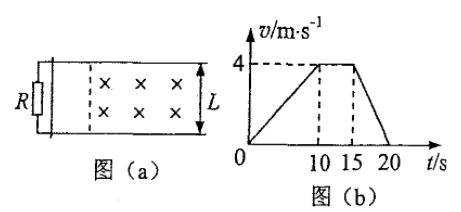
(1)金属杆所受拉力的大小为 ;
(2) 匀强磁场的磁感应强度大小为 ;
(3) 内磁感应强度随时间的变化规律。
质量为
的小球在竖直向上的恒定拉力作用下,由静止开始从水平地面向上运动,经一段时间,拉力做功为
,此后撤去拉力,球又经相同时间回到地面,以地面为零势能面,不计空气阻力。求:
(1)球回到地面时的动能
;
(2)撤去拉力前球的加速度大小
及拉力的大小
;
(3)球动能为
/5时的重力势能
。
如图,气缸左右两侧气体由绝热活塞隔开,活塞与气缸光滑接触。初始时两侧气体均处于平衡态,体积之比 ,温度之比 。先保持右侧气体温度不变,升高左侧气体温度,使两侧气体体积相同;然后使活塞导热,两侧气体最后达到平衡,求:

(1)两侧气体体积相同时,左侧气体的温度与初始温度之比;
(2)最后两侧气体的体积之比。