在 中,满足
中,满足 ,
,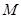 是
是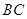 中点.
中点.
(1)若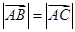 ,求向量
,求向量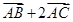 与向量
与向量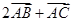 的夹角的余弦值;
的夹角的余弦值;
(2)若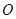 是线段
是线段 上任意一点,且
上任意一点,且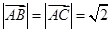 ,求
,求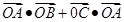 的最小值;
的最小值;
(3)若点 是
是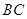 边上一点,且
边上一点,且 ,
,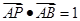 ,
, ,求
,求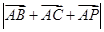 的最小值.
的最小值.
命题 实数
实数 满足
满足 ,其中
,其中 ,命题
,命题 实数
实数 满足
满足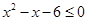 或
或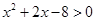 ,且
,且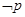 是
是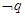 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备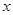 年的年平均污水处理费用
年的年平均污水处理费用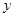 (万元);
(万元);
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
(1)求与双曲线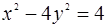 有共同的渐近线,且过点
有共同的渐近线,且过点 的双曲线的方程。
的双曲线的方程。
(2)已知中心在原点,一焦点为F(0,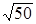 )的椭圆被直线L:y=3x-2截得的弦的中点的横坐标为
)的椭圆被直线L:y=3x-2截得的弦的中点的横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。
解不等式:|x-1|+|x+2|≥5.
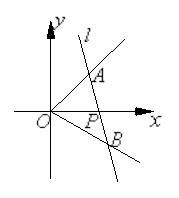
如图,在直角坐标系中,射线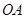 :
: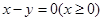 ,
,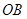 :
: ,
,
过点 作直线分别交射线
作直线分别交射线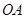 、
、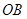 于
于 、
、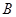 点.
点.
(1)当 的中点为
的中点为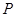 时,求直线
时,求直线 的方程;
的方程;
(2)当 的中点在直线
的中点在直线 上时,求直线
上时,求直线 的方程.
的方程.