若sin α＋sin β＋sin γ＝0，cos α＋cos β＋cos γ＝0，则cos(α－β)＝( )．
| A．1 | B．－1 | C． |
D．－ |
p＝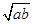
＋
，q＝
·
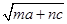(m、n、a、b、c、d均为正数)，
则p、q的大小为 ( )
| A．p≥q | B．p≤q | C．p＞q | D．不确定 |
设x，y∈R，且4xy＋4y2＋x＋6＝0，则x的取值范围是 ( )
| A．－3≤x≤2 | B．－2≤x≤3 |
| C．x≤－2或x≥3 | D．x≤－3或x≥2 |
已知a，b，c是三条互不重合的直线，α，β是两个不重合的平面，给出
四个命题：①a∥b，b∥α，则a∥α；②a，b⊂α，a∥β，b∥β，则α∥β；③a⊥α，a∥β，则α⊥β；④a⊥α，b∥α，则a⊥b.
其中正确的命题个数是 ( )
| A．1 | B．2 | C．3 | D．4 |
设x，y，z∈(0，＋∞)，a＝x＋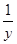
，b＝y＋
，c＝z＋
，则a，b，c三数( )
| A．至少有一个不大于2 | B．都小于2 |
| C．至少有一个不小于2 | D．都大于2 |
的值是（ ） 
