一个手机经销商计划购进某品牌的A型、B型、C型手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部、三款手机的进价和预售价如下表:
手机型号 A型 B型 C型进价(单位:元/部) 900 1200 1100
预售价(单位:元/部) 1200 1600 1300用含x的式子表示购进B、C两种型号手机的总数
该经销商共有几种进货方案;
哪种方案可获利最多,最多可获利多少元?
(1)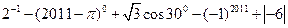
(2)解不等式组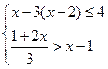 ,并用数轴表示解集.
,并用数轴表示解集.
已知抛物线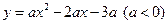 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B的坐标;
(2)过点D作DH丄y轴于点H,若DH=HC,求a的值和直线CD的解析式;
(3)在第(2)小题的条件下,直线CD与x轴交于点E,过线段OB的中点N作NF丄x轴,并交直线CD于点F,则直线NF上是否存在点M, 使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.
使得点M到直线CD的距离等于点M到原点O的距离?若存在,求出点M的坐标;若不存在,请说明理由.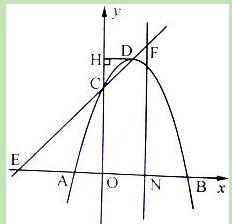
如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=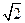 ,求EB的长.
,求EB的长.
上个月某超市购进了两批相同品种的水果,第一批用了2000元,第二批用了5500元,第二批购进水果的重量是第一批的2.5倍,且进价比第一批每千克多1元.
(1)求两批水果共购进了多少千克?
(2)在这两批水果总重量正常损耗10%,其余全部售完的情况下,如果这两批水果的售价相同,且总利润率不低于26%,那么售价至少定为每千克多少元?
(利润率= )
)
一个不透明的纸盒中装有大小相同的黑、白两种颜色的围棋,其中白色棋子3个(分别用白A、白B、白C表示),若从中任意摸出一个棋子,是白色棋子的概率为 .
.
(1)求纸盒中黑色棋子的个数;
(2)第一次任意摸出一个棋子(不放回),第二次再摸出一个棋子,请用树状图或列表的方法,求两次摸到相同颜色棋子的概率.