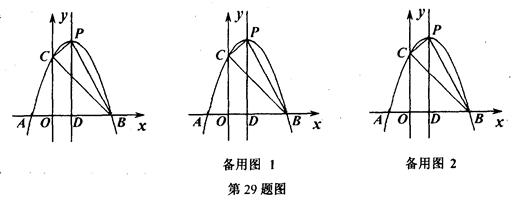
如图,抛物线y=ax2+bx+c的顶点为P,对称轴直线x=1与x轴交于点D,抛物线与x轴交于A、B两点,与y轴交于点C,其中A(-1,0)、C(0,3).求此抛物线的解析式
点E在线段BC上,若△DEB为等腰三角形,求点E的坐标
点F、Q都在该抛物线上,若点C与点F关于直线x=1成轴对称,连结BF、BQ,如果∠FBQ=45°,求点Q的坐标;
将△BOC绕着它的顶点B顺时针在第一象限内旋转,旋转后的图形为△BO'C',BO'与BP重合时,则△BO'C'不在BP上的顶点C'的坐标为 ▲ (直接写出答案).
先化简,再求值:2x2-(3x2-2y)+5(x2-y),其中x=-1,y=2.
解方程:
(1)4x-5=x+7
(2)4(2x-3)-(5x-1)=7
(3)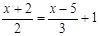
(4)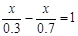
计算:
(1)
(2)
(3)3f + 2f-6f
(4)x-y-(5x-4y)
如图1是立方体和长方体模型,立方体棱长和长方体底面各边长都为1,长方体侧棱长为2,现用60张长为6,宽为4的长方形卡纸,剪出这两种模型的表面展开图,有两种方法:
方法一:如图2,每张卡纸剪出3个立方体表面展开图;
方法二:如图3,每张卡纸剪出2个长方体表面展开图(图中只画出1个).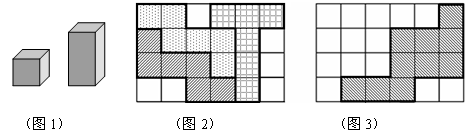
设用x张卡纸做立方体,其余卡纸做长方体,共做两种模型y个.要求制作的长方体的个数不超过立方体的个数.
(1)在图3中画出第二个长方体表面展开图,用阴影表示;
(2)请你写出y关于x的函数解析式,并注明自变量x的取值范围;
(3)设每只模型(包括立方体和长方体)平均获利为w(元),w满足函数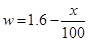 ,
,
若想将模型作为教具卖出获得最大利润,则应该制作立方体和长方体各多少个?最大利润是多少?
如图,在边上为1个单位长度的小正方形网格中: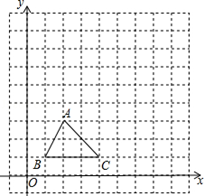
(1)画出△ABC向上平移6个单位长度,再向右平移 5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.