已知：图1为一锐角是30°的直角三角尺，其边框为透明塑料制成(内、外直角三角形对应边互相平行且三处所示宽度相等)．操作：将三角尺移向直径为4cm的⊙O，它的内Rt△ABC的斜边AB恰好等于⊙O的直径，它的外Rt△A′B′C′的直角边A′C′ 恰好与⊙O相切(如图2)。
思考：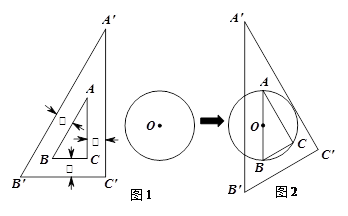
求直角三角尺边框的宽
求证：
BB′C′+CC′B′=75°。求边B′C′的长。
（1）已知∠AOB是直角，OM平分∠AOC，ON平分∠BOC，求∠MON与∠AOB的关系．
（2）如果（1）中，改变∠AOB的大小，其他条件不变，求∠MON与∠AOB的关系．
（3）你从（1），（2）的结果中能发现什么规律？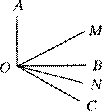
如图,已知直线AB和CD相交于O点,OC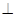
OE ,OF 平分∠AOE, ∠COF=34°,求∠BOD的度数.
已知A、B两家商店的随身听的单价相同，书包的单价也相同，随身听和书包的单价之和为452元，且随身听的单价比书包的单价的4倍少8元．
(1)问随身听和书包的单价各是多少元?
(2)现在这两家商店搞促销，促销方式如下：
商店A：所有的商品打八折销售；
商店B：每购物满100元，立即返还25元(例如，购物205元，则立即返还50元)．
小明身上带了400元钱，想买随身听和书包各一个，那么，他应该选择在哪一家商店购买更省钱?
如图，OE⊥AB，垂足为O，OF平分∠BOD，∠DOE∶∠EOC＝1∶2，求∠AOF的度数．
先化简，再求值：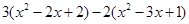
，其中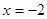
.