已知一次函数y1 = 2x和二次函数y2 = x2 + 1。求证:函数y1、y2的图像都经过同一个定点;
求证:在实数范围内,对于任意同一个x的值,这两个函数所对应的函数值y1 ≤ y2总成立;
是否存在抛物线y3 = ax2 + bx + c,其图象经过点(
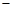 5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
5,2),且在实数范围内,对于同一个x的值,这三个函数所对应的函数值y1 ≤ y3 ≤ y2总成立?若存在,求出y3的解析式;若不存在,说明理由。
近年某高中招生制度改革,实行自主招生。某初中学校获得保送(指标生)名额若干,现在九年级四位品学兼优的学生小斌(男)、小亮(男)、小红(女)、小丽(女)都获得保送资格,且机会均等。
(1)、若学校只有一个名额,则随机选到小斌的概率是
(2)、若学校争取到两个名额,请用树状图或列表法求随机选到保送的学生恰好是一男一女的概率。
先化简,后求值: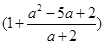
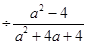 ,其中
,其中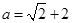
如图,在△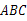 中,∠
中,∠ 90°,
90°, ,
, ,点
,点 从点
从点 出发,沿
出发,沿 以
以
2㎝ 的速度向点
的速度向点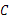 移动,点
移动,点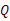 从点
从点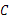 出发,以
出发,以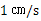 的速度向点
的速度向点 移动,若点
移动,若点 分别从点
分别从点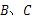 同时出发,
同时出发,
设运动时间为 ,当
,当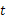 为何值时,△
为何值时,△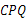 与△
与△ 相似?
相似?
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元。为了扩大销售,增加盈利,商场决定采取适当的降价措施。经调查发现,在一定范围内,衬衫的单价每降一元,商场平均每天可多售出2件。
(1)如果商场通过销售这批衬衫每天要盈利1200元,衬衫的单价应降多少元?
(2)在上述条件不变、销售正常情况下,每件商品降价多少元是,商场盈利W最多?
有一道练习题是:对于式子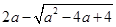 先化简,后求值,其中
先化简,后求值,其中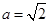 .
.
小明的解法如下: 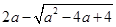 =
=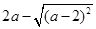 =
=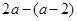 =
=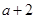 =
=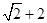 .
.
小明的解法对吗?如果不对,请改正.