在平面直角坐标系xOy中,O为坐标原点,直线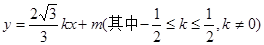 经过点A(
经过点A(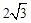 ,4),且与
,4),且与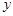 轴相交于点C. 点B在
轴相交于点C. 点B在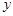 轴上,且
轴上,且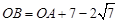 . △ABC的面积为S.
. △ABC的面积为S.求m的取值范围;
求S关于m的函数关系式;
设点B在
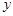 轴的正半轴上,当S取得最大值时,将△ABC沿AC折叠得到
轴的正半轴上,当S取得最大值时,将△ABC沿AC折叠得到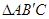 ,求点
,求点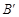 的坐标.
的坐标.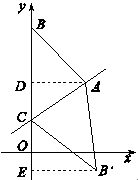
某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“ 30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
为了解某住宅区的家庭用水量情况,从该住宅区中随机抽样调查了50户家庭去 年每个月的用水量,统计得到的数据绘制了下面的两幅统计图.图1是去年这50户家庭月总用水量的折线统计图,图2是去年这50户家庭月总用水量的不完整的频数分布直方图.
年每个月的用水量,统计得到的数据绘制了下面的两幅统计图.图1是去年这50户家庭月总用水量的折线统计图,图2是去年这50户家庭月总用水量的不完整的频数分布直方图.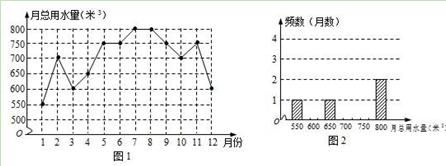
(1)根据图1提供的信息,补全图2中的频数分布直方图 ;
;
(2)在抽查的50户家庭去年月总用水量这12个数据中,极差是____ ,众数是____
,众数是____ ,中位数是____
,中位数是____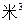 ;
;
(3)请你根据上述提供的统计数据,估计该住宅区今年每户家庭平均每月的用水量是多少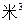 ?
?
为了美化都匀市环境,打造中国优秀旅游城市,现欲将剑江河进行清淤疏通改造,现有两家清淤公司可供选择,这两家公司提供信息如表所示: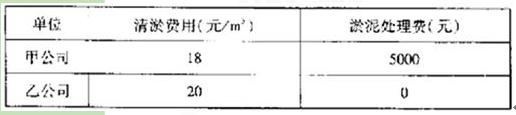
(1)若剑江河首批需要清淤的淤泥面积大约为1.2万平方米,平均厚度约为0.4米,那么请哪个清淤公司进行清淤费用较省,请说明理由(体积可按面积×高进行计算)
(2)若甲公司单独做了2天,乙公司单独做了3天,恰好完成全部清淤任务的一半;若甲公司先做2天,剩下的清淤工作由乙公司单独完成,则乙公司所用时间恰好比甲公司单独完成清淤任务所用时间多1天,则甲、乙两公司单独完成清淤任务各需多少时间?
北京时间2011年3月11日46分,日本东部海域发生9级强烈地震并引发海啸.在其灾区,某药品的需求量急增.如图所示,在平常对某种药品的需求量y1(万件).供应量y2(万件)与价格x(元∕件)分别近似满足下列函数关系式: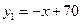 ,
,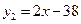 ,需求量为0时,即停止供应.当
,需求量为0时,即停止供应.当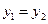 时,该药品的价格称为稳定价格,需求量称为稳定需求量.
时,该药品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该药品的稳定价格与稳定需求量.
(2)价格在什么范围内,该药品的需求量低于供应量?
(3)由于该地区灾情严重,政府部门决定对药品供应方提供价格补贴来提高供货价格,以提高供应量.根据调查统计,需将稳定需求量增加6 万件,政府应
万件,政府应 对每件药品提供多少元补贴,才能使供应量等于需求量.
对每件药品提供多少元补贴,才能使供应量等于需求量.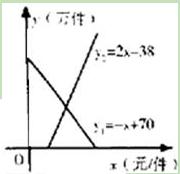
(1)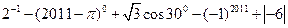
(2)解不等式组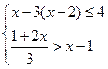 ,并用数轴表示解集.
,并用数轴表示解集.