列方程组解下列应用题．（每小题8分，共16分）
(1) 甲、乙两人分别以均匀的速度在400米圆形跑道上跑步，甲的速度较快．当两人反向跑时，每40秒钟相遇一次；当两人同向跑时，每3分20秒相遇一次，求甲、乙两人的速度．
(2) 某市政府决定2012年投入6000万元用于改善医疗卫生服务，比2011年增加了1250万元．投入资金的服务对象包括“需方”（患者等）和“供方”（医疗卫生机构等），预计2012年投入“需方”的资金比2011年提高30%，投入“供方”的资金将比2011年提高20%．该市政府2011年投入“需方”和“供方”的资金各是多少万元？
如图，已知矩形OABC中，OA=2，AB=4，双曲线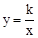
（k＞0）与矩形两边AB、BC分别交于E、F．
（1）若E是AB的中点，求F点的坐标；
（2）若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值．
如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．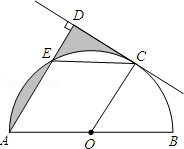
（1）判断CD与⊙O的位置关系，并证明你的结论；
（2）若E是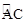
的中点，⊙O的半径为1，求图中阴影部分的面积．
为了从甲、乙两名选手中选拔一个参加射击比赛，现对他们进行一次测验，两个人在相同条件下各射靶10次，为了比较两人的成绩，制作了如下统计图表：
甲、乙射击成绩统计表
| 平均数 |
中位数 |
方差 |
命中10环的次数 |
|
| 甲 |
7 |
|
|
0 |
| 乙 |
|
|
|
1 |
甲、乙射击成绩折线图
（1）请补全上述图表（请直接在表中填空和补全折线图）；
（2）如果规定成绩较稳定者胜出，你认为谁应胜出？说明你的理由；
（3）如果希望（2）中的另一名选手胜出，根据图表中的信息，应该制定怎样的评判规则？为什么？
解方程：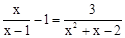
．
如图，在平面直角坐标系中，点A、B在x轴上，点C、D在y轴上，且OB=OC=3，OA=OD=1，抛物线y=ax2+bx+c（a≠0）经过A、B、C三点，直线AD与抛物线交于另一点M．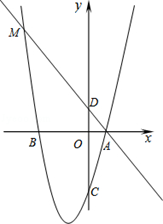
（1）求这条抛物线的解析式；
（2）P为抛物线上一动点，E为直线AD上一动点，是否存在点P，使以点A、P、E为顶点的三角形为等腰直角三角形？若存在，请求出所有点P的坐标；若不存在，请说明理由．
（3）请直接写出将该抛物线沿射线AD方向平移
个单位后得到的抛物线的解析式．