某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为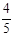 ,第二、第三门课程取得优秀成绩的概率分别为
,第二、第三门课程取得优秀成绩的概率分别为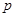 ,
, (
(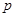 >
> ),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为
| ξ |
0 |
1 |
2 |
3 |
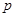 |
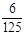 |
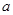 |
b |
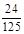 |
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求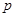 ,
, 的值;
的值;
(Ⅲ)求数学期望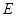 ξ.
ξ.
(本小题满分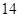 分)
分)
若函数 在定义域
在定义域 内某区间
内某区间 上是增函数,而
上是增函数,而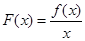 在
在 上是减函数,
上是减函数,
则称 在
在 上是“弱增函数”
上是“弱增函数”
(1)请分别判断 =
= ,
, 在
在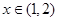 是否是“弱增函数”,
是否是“弱增函数”,
并简要说明理由;
(2)证明函数 (
(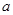 是常数且
是常数且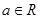 )在
)在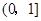 上是“弱增函数”.
上是“弱增函数”.
(本小题满分 分)设函数
分)设函数 的最高点
的最高点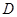 的坐标为(
的坐标为( ),由最高点
),由最高点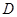 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与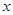 的交点的坐标为(
的交点的坐标为( ).
).
(1)求函数 的解析式.
的解析式.
(2)当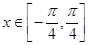 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量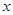 的值.
的值.
(3)将函数 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数 的单调减区间.
的单调减区间.
(本小题满分 分)已知
分)已知 ,
, ;
;
(1) 若 ,求
,求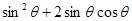 的值;
的值;
(2)若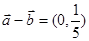 ,
,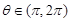 ,求
,求 的值.
的值.
(本题满分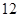 分)已知函数
分)已知函数 .
.
(1)求 与
与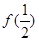 ,
,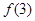 与
与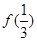 ;
;
(2)由(1)中求得结果,你能发现 与
与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论;
(3)求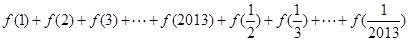 的值 .
的值 .
(本小题满分 分)
分)
(1)化简 .
.
(2)求函数 的最大值及相应的
的最大值及相应的 的值.
的值.