如图1,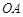 、
、 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段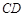 和曲线段
和曲线段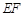 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥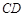 上某点
上某点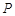 分别修建与
分别修建与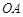 、
、 平行的栈桥
平行的栈桥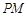 、
、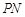 ,且以
,且以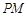 、
、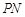 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台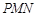 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段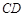 的方程是
的方程是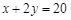
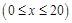 ,曲线段
,曲线段 的方程是
的方程是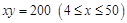 ,设点
,设点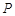 的坐标为
的坐标为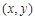 ,记
,记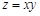 (题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度).
(1)求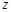 的取值范围;
的取值范围;
(2)试写出三角形观光平台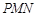 面积
面积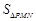 关于
关于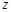 的函数解析式,并求出该面积的最小值.
的函数解析式,并求出该面积的最小值.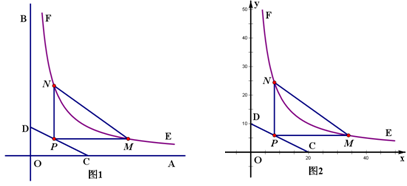
数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,对于任意
项和,对于任意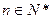 ,总有
,总有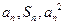 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列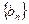 的前
的前 项和为
项和为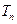 ,且
,且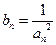 ,求证:对任意正整数
,求证:对任意正整数 ,总有
,总有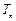
 2;
2;
(Ⅲ)正数数列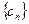 中,
中,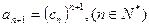 ,求数列
,求数列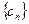 中的最大项.
中的最大项.
已知函数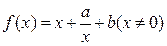 ,其中
,其中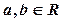 .
.
(Ⅰ)若曲线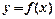 在点
在点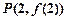 处的切线方程为
处的切线方程为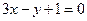 ,求函数
,求函数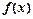 的解析;
的解析;
(Ⅱ)对任意的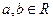 ,求函数
,求函数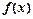 的单调区间.
的单调区间.
青岛第一海水浴场位于汇泉湾畔,拥有长580米,宽40余米的沙滩,是亚洲较
大的海水浴场.这里三面环山,绿树葱茏,现代的高层建筑与传统的别墅建筑巧妙地结合在
一起,景色非常秀丽.海湾内水清浪小,滩平坡缓,沙质细软,自然条件极为优越.
已知海湾内海浪的高度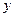 (米)是时间
(米)是时间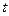 (
(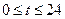 ,单位:小时)的函数,记作
,单位:小时)的函数,记作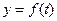 .下表是某日
.下表是某日 各时刻记录的浪高数据:
各时刻记录的浪高数据:
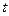 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
 |
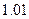 |
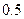 |
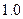 |
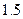 |
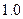 |
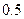 |
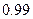 |
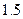 |
经长期观测,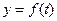 的曲线可近似地看成是函数
的曲线可近似地看成是函数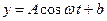 的图象.
的图象.
(Ⅰ)根据以上数据,求函数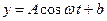 的最小正周期
的最小正周期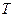 ,振幅
,振幅 及函数表达式;
及函数表达式;
(Ⅱ)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内从上午8∶00至晚上20∶00之间,哪段时间可对冲浪爱好者开放 ?
?
已知数列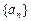 满足:
满足: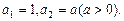 数列
数列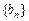 满足
满足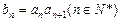 .
.
(Ⅰ)若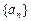 是等差数列,且
是等差数列,且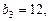 求
求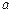 的值及
的值及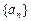 的通项公式;
的通项公式;
(Ⅱ)若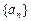 是等比数列,求
是等比数列,求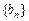 的前项和
的前项和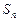 .
.
已知函数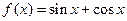 ,
,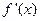 是
是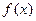 的导函数.
的导函数.
(Ⅰ)求函数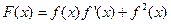 的最大值和相应的
的最大值和相应的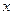 值;
值;
(Ⅱ)若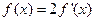 ,求
,求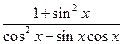 的值.
的值.