青岛第一海水浴场位于汇泉湾畔,拥有长580米,宽40余米的沙滩,是亚洲较
大的海水浴场.这里三面环山,绿树葱茏,现代的高层建筑与传统的别墅建筑巧妙地结合在
一起,景色非常秀丽.海湾内水清浪小,滩平坡缓,沙质细软,自然条件极为优越.
已知海湾内海浪的高度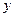 (米)是时间
(米)是时间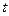 (
(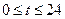 ,单位:小时)的函数,记作
,单位:小时)的函数,记作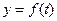 .下表是某日
.下表是某日 各时刻记录的浪高数据:
各时刻记录的浪高数据:
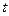 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
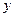 |
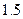 |
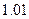 |
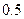 |
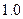 |
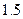 |
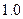 |
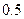 |
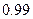 |
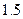 |
经长期观测,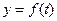 的曲线可近似地看成是函数
的曲线可近似地看成是函数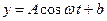 的图象.
的图象.
(Ⅰ)根据以上数据,求函数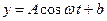 的最小正周期
的最小正周期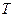 ,振幅
,振幅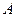 及函数表达式;
及函数表达式;
(Ⅱ)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内从上午8∶00至晚上20∶00之间,哪段时间可对冲浪爱好者开放 ?
?
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据。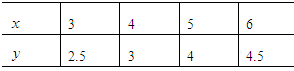
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ;
;
(2)已知该厂技改前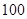 吨甲产品的生产能耗为
吨甲产品的生产能耗为 吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨标准煤.试根据(2)求出的线性回归方程,预测生产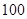 吨甲产品的生产能耗比技改前降低多少吨标准煤?
吨甲产品的生产能耗比技改前降低多少吨标准煤?
(线性回归方程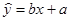 中的系数
中的系数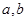 可以用公式
可以用公式 )
)
(本小题满分12分)
在平面直角坐标系xOy中,曲线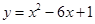 与坐标轴的交点都在圆C上
与坐标轴的交点都在圆C上
(1)求圆C的方程;
(2)若圆C与直线 交与A,B两点,且
交与A,B两点,且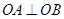 ,求a的值。
,求a的值。
(本小题满分12分)已知点P和点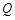 是曲线
是曲线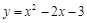 上的两点,且点
上的两点,且点 的横坐标是1,点
的横坐标是1,点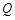
的横坐标是4,求:(1)割线的
 斜率;(2)点
斜率;(2)点 处的切线方程.
处的切线方程.
(本小题满分10分)求以椭圆 的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
(满分12分)3.已知数列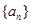 的前
的前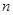 项和为
项和为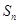 ,且有
,且有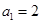 ,
,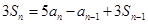

(1)求数列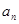 的通项公式;
的通项公式;
(2)若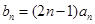 ,求数列
,求数列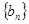 的前
的前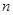 项的和
项的和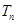 。山大附中
。山大附中