如图,某机场建在一个海湾的半岛上,飞机跑道AB的长为4.5km,且跑道所在的直线与海岸线l的夹角为60o(海岸线可以看作是直线),跑道上离海岸线距离最近的点B到海岸线的距离BC=4 km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
km.D为海湾一侧海岸线CT上的一点,设CD=x(km),点D对跑道AB的视角为q.
(1)将tanq表示为x的函数;
(2)求点D的位置,使q取得最大值.

如图,在直角梯形 中,
中,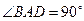 ,
,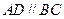 ,
,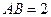 ,
,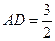 ,
,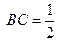 ,椭圆以
,椭圆以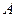 、
、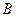 为焦点且经过点
为焦点且经过点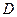 .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系。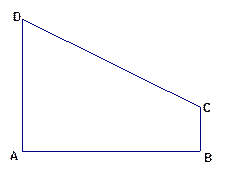
在等差数列 中,
中, ,
,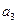 与
与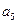 的一个等比中项为
的一个等比中项为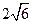 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的通项
的通项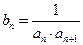 ,求数列
,求数列 的前
的前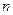 项和
项和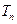 。
。
下表为某体育训练队跳高、跳远成绩的分布,共有队员40人,成绩分为1~5五个档次。例如表中所示跳高成绩为4分,跳远成绩为2分的队员为5人.将全部队员的姓名卡混合在一起,任取一张,该卡片队员的跳高成绩为x分,跳远成绩为y分.
⑴求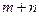 的值;
的值;
⑵求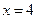 的概率及
的概率及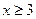 且
且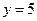 的概率.
的概率.
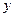  |
跳远 |
|||||
| 5 |
4 |
3 |
2 |
1 |
||
跳 高 |
5 |
1 |
3 |
1 |
0 |
1 |
| 4 |
1 |
0 |
2 |
5 |
1 |
|
| 3 |
2 |
1 |
0 |
4 |
3 |
|
| 2 |
1 |
 |
6 |
0 |
 |
|
| 1 |
0 |
0 |
1 |
1 |
3 |
已知 中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
中∠ACB=90°,SA⊥面ABC,AD⊥SC于D,
求证: AD⊥面SBC;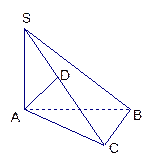
已知向量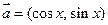 ,
,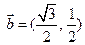 ,函数
,函数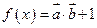 。
。
(Ⅰ)求函数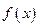 的值域;
的值域;
(Ⅱ)当 ,且
,且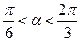 时,求
时,求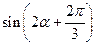 的值
的值