如图,在直角梯形 中,
中,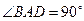 ,
,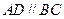 ,
,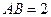 ,
,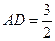 ,
,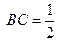 ,椭圆以
,椭圆以 、
、 为焦点且经过点
为焦点且经过点 .
.
(Ⅰ)建立适当的直角坐标系,求椭圆的方程;
(Ⅱ)以该椭圆的长轴为直径作圆,判断点C与该圆的位置关系。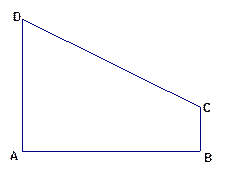
等差数列
中,
,
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)设
,求
的值.
已知
,函数
的最小值为
.
(Ⅰ)求
的值;
(Ⅱ)求
的最小值.
选修4-4:坐标系与参数方程
在平面直角坐标系
中,圆
的参数方程为
.在极坐标系(与平面直角坐标系
取相同的长度单位,且以原点
为极点,以
轴非负半轴为极轴)中,直线
的方程为
.
(Ⅰ)求圆
的普通方程及直线
的直角坐标方程;
(Ⅱ)设圆心
到直线
的距离等于2,求
的值.
已知矩阵
(Ⅰ)求
的逆矩阵
;
(Ⅱ)求矩阵
,使得
.
已知函数 ,
(Ⅰ)证明:当
;
(Ⅱ)证明:当
时,存在
,使得对
(Ⅲ)确定
的所以可能取值,使得存在
,对任意的
恒有
.