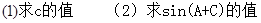已知,函数的最小值为.
(Ⅰ)求的值;
(Ⅱ)求的最小值.
已知等差数列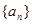
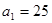 ,
,
(1) 求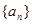 的通项公式;
的通项公式;
(2) 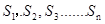 哪一个最大?并求出最大值
哪一个最大?并求出最大值
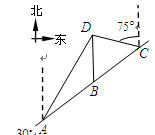
如图,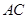 是佛山市一环东线的一段,其中
是佛山市一环东线的一段,其中 、
、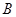 、
、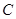 分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界
分别是林上路、佛陈路、花卉大道出口,经测量陈村花卉世界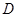 位于点
位于点 的北偏东
的北偏东 方向
方向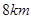 处,位于点
处,位于点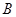 的正北方向,位于点
的正北方向,位于点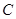 的北偏西
的北偏西 方向上,并且
方向上,并且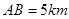 .
.
(1) 求佛陈路出口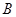 与花卉世界
与花卉世界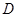 之间的距离;(精确到0.1km)
之间的距离;(精确到0.1km)
(2) 求花卉大道出口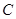 与花卉世界
与花卉世界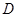 之间的距离.(精确到0.1km)
之间的距离.(精确到0.1km)
(参考数据: ,
, ,
,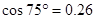 ,
,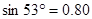 ,
,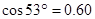 ,
, 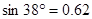 ,
,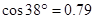
某人一次同时抛掷两枚均匀骰子(它们的六个面分别标有点数1、2、3、4、5、6)
求:(1)两枚骰子点数相同的概率;
(2)两枚骰子点数和为5的倍数的概率。
已知 ,
,  , 函数f(x)=
, 函数f(x)= 
(1)求函数 的单调增区间。
的单调增区间。
(2)求函数 的最大值及
的最大值及 取最大值时x的集合。
取最大值时x的集合。
已知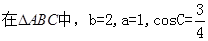 .
.