为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图: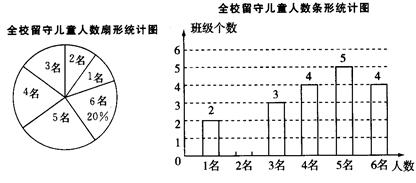
求该校平均每班有多少名留守儿童?并将该条形统计图补充完整.
某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
如图,∠A=∠B,CE∥DA,CE交AB于E.求证:△CEB是等腰三角形.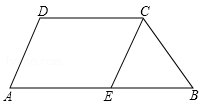
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕着点C旋转到如图1所示的位置时,求证:①△ADC≌△CEB; ②DE=AD+BE;
(2)当直线MN绕着点C旋转到如图2所示的位置时,①找出图中一对全等三角形;②DE、AD、BE之间有怎样的数量关系,并加以证明.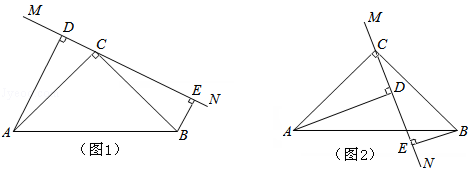
在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若AB=5,求线段DE的长.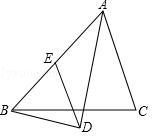
如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.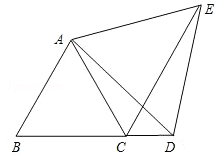
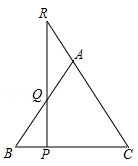
如图,P是等腰三角形ABC底边BC上的一个动点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R.请观察AR与AQ,它们有何关系?并证明你的猜想.