班主任让同学们为班会活动设计一个抽奖方案，拟使中奖概率为60%．小明的设计方案：在一个不透明的盒子中，放入10个球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，摸到黄球则表示中奖，否则不中奖．如果小明的设计符合老师要求，则盒子中黄球应有 ▲ 个，白球应有 ▲ 个；
小兵的设计方案：在一个不透明的盒子中，放入4个黄球和1个白球，这些球除颜色外都相同，搅匀后从中任意摸出2个球，摸到的2个球都是黄球则表示中奖，否则不中奖．该设计方案是否符合老师的要求？试说明理由．
已知m=2010×2011﹣1，n=20102﹣2010×2011+20112，请尝试用一种简便方法比较m、n大小．
已知|x﹣y+1|与x2+8x+16互为相反数，求x2+2xy+y2的值．
设实数a，b，c满足a2+b2+c2=1．若a+b+c=0，求ab+bc+ca的值；
先阅读下面的内容，再解决问题，
例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值．
解：∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴（m+n）2+（n﹣3）2=0
∴m+n=0，n﹣3=0
∴m=﹣3，n=3
问题（1）若x2+2y2﹣2xy+4y+4=0，求xy的值．
（2）已知a，b，c是△ABC的三边长，满足a2+b2=10a+8b﹣41，且c是△ABC中最长的边，求c的取值范围．
已知a=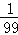
x+2009，b=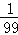x+2008，c=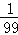x+2010，求代数式a2+b2+c2﹣ab﹣bc﹣ca的值．