小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡底跑到坡顶再原路返回坡底.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).
小亮下坡的速度是 ▲ m/min;= ▲
求出AB所在直线的函数关系式
如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.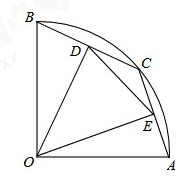
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
如图,已知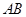 为
为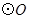 的直径,
的直径, 是
是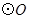 的切线,
的切线, 为切点,
为切点,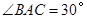
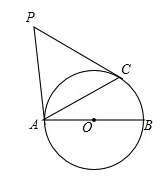
(Ⅰ)求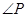 的大小;
的大小;
(Ⅱ)若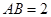 ,求
,求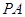 的长(结果保留根号).
的长(结果保留根号).
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.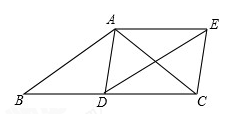
(1)求证:△ADC≌△ECD;
(2)若BD=CD,求证:四边形ADCE是矩形.
在等腰△ABC中,三边分别为a、b、c,其中a=5,若关于x的方程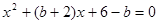 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
(1)x2+2x=1
(2)x(x﹣3)=x﹣3