如图，已知抛物线与x轴交于点A(-2,0),B(4,0)，与y轴交于点C(0,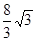
)．
求抛物线的解析式及其顶点D的坐标；
设直线CD交x轴于点E，过点B作x轴的垂线，交直线CD于点F，在直线CD的上方，y轴及y轴的右侧的平面内找一点G，使以点G、F、C为顶点的三角形与△COE相似，请直接写出符合要求的点G的坐标；
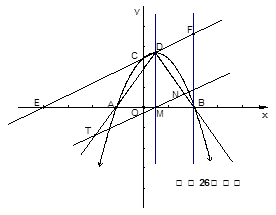
如图，抛物线的对称轴与x轴的交点M，过点M作一条直线交∠ADB于T,N两点，①当∠DNT=90°时，直接写出
的值；
②当直线TN绕点M旋转时，
试说明: △DNT的面积S△DNT=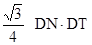
;
并猜想 :的值是否是定值?说明理由.
七年级一班某次数学测验的平均成绩为80分，数学老师以平均成绩为基准，记作0，把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10，–15，0，+20，–2．问这五位同学的实际成绩分别是多少分？
如图两个椭圆分别表示正数集合和整数集合（1）请在每个圈内填入6个数；（2）其中有3个数既是正数又是整数这3个数应填在______处（A，B，C）你能说出两个圈重叠部分表示什么数的集合吗？
简答题：
（1）－1和0之间还有负数吗？如有，请列举。
（2）－3和－1之间有负整数吗？－2和2之间有哪些整数？
（3）有比－1大的负整数吗？有比1小的正整数吗？
（4）写出三个大于－105小于－100的有理数。
把下面的直线补充成一条数轴，然后在数轴上标出下列各数：
–3，+l，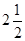
，－l.5，6.
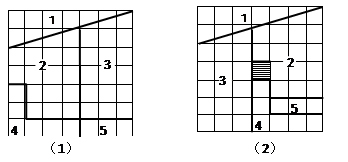
把一张方格纸贴在纸板上．按图1所示画上正方形，然后沿图示的直线切成5小块．当你照图2的样子把这些拼成正方形的时候中间居然出现了一个洞！
我们发现，图1的正方形是由49个小正方形组成的．图2中拼成的正方形却只有48个小正方形．哪一个小正方形没有了？它到哪去了？