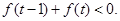将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为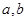 .
.
(1)求直线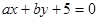 与圆
与圆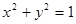 相切的概率;
相切的概率;
(2)将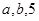 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
(本小题满分14分)
(1)已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
(2)已知圆C的圆心是直线 和
和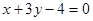 的交点且与直线
的交点且与直线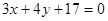 相切,求圆C的方程.
相切,求圆C的方程.
(本小题满分14分) 已知函数
(1)求函数 的最小正周期;
的最小正周期;
(2)确定函数 在
在 上的单调性并求在此区间上
上的单调性并求在此区间上 的最小值.
的最小值.
(本小题满分12分)某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
(本小题满分12分)已知平面向量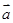
 ,
,

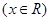 .
.
(1)若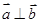 ,求
,求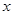 的值;
的值;
(2)若 ,求|
,求|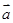 -
- |.
|.
已知函数 是定义在(-1, 1)上的奇函数,且
是定义在(-1, 1)上的奇函数,且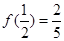 ,
,
(1)确定函数的解析式;
(2)用定义法判断函数的单调性;
(3)解不等式;