椭圆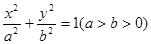
与
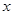轴负半轴交于点
，
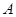为椭圆第一象限上的点，直线
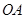交椭圆于另一点
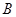，椭圆左焦点为
，连接
交
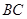于点D。
（1）如果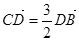
，求椭圆的离心率；
（2）在（1）的条件下，若直线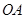的倾斜角为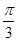
且△ABC的面积为
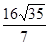，求椭圆的标准方程。
如图在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，过D与PB垂直的平面分别交PB、PC于F、E。PD=DC。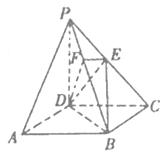
（1）求证：DE⊥PC
（2）求证：PA//平面EDB；
（3）求二面角C—PB—D的大小。
已知函数
时取最大值2。
是集合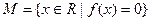
中的任意两个元素，
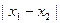的最小值为。
（1）求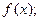
（2）若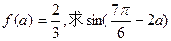
的值。
过点P(-2,-3)作圆C:(x-4)2+(y-2)2=9的两条切线,切点分别为A、B.求:
(1)经过圆心C,切点A、B这三点的圆的方程;
(2)直线AB的方程;
(3)线段AB的长.
圆心在直线5x-3y-8=0上的圆与两坐标轴相切,求此圆的方程.
求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点，且满足下列条件之一的圆的方程.
(1)过原点;
(2)有最小面积.