已知极点与坐标原点O重合,极轴与x轴非负半轴重合,M是曲线C: 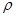 =4sin
=4sin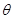 上任一点,点P满足
上任一点,点P满足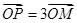 .设点P的轨迹为曲线Q.
.设点P的轨迹为曲线Q.
(1)求曲线Q的方程;
(2)设曲线Q与直线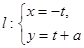 (t为参数)相交于A、B两点,且|AB|=4.求实数a.
(t为参数)相交于A、B两点,且|AB|=4.求实数a.
(本小题满分12分)已知定义在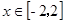 上的偶函数
上的偶函数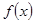 满足:当
满足:当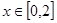 时,
时,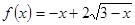 .
.
(1)求函数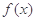 在
在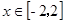 上的解析式;
上的解析式;
(2)设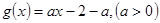 ,若对于任意
,若对于任意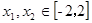 ,都有
,都有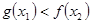 成立,求实数
成立,求实数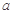 的取值范围.
的取值范围.
(本小题满分12分)已知函数 ,
,
(1)当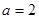 时,求函数
时,求函数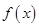 在
在 上的值域;
上的值域;
(2)若 ,求使函数
,求使函数 的定义域为
的定义域为 ,值域为
,值域为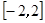 的
的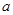 的值;
的值;
(本小题满分12分)如图,长方体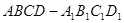 中,
中,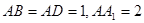 ,点
,点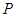 为棱
为棱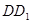 上一点.
上一点.
(1)求证:平面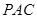 ⊥平面
⊥平面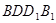 ;
;
(2)若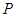 是棱
是棱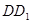 的中点,求
的中点,求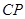 与平面
与平面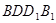 所成的角大小.
所成的角大小.
已知函数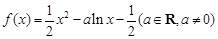 .
.
(Ⅰ)当 时,求曲线
时,求曲线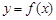 在点
在点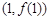 处的切线方程;
处的切线方程;
(Ⅱ)求函数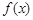 的单调区间;
的单调区间;
(Ⅲ)若对任意的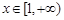 ,都有
,都有 成立,求a的取值范围.
成立,求a的取值范围.
某厂生产产品x件的总成本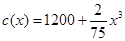 (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为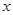 件时,总利润为
件时,总利润为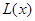 (万元),求
(万元),求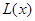 的解析式;
的解析式;
(2)产量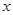 定为多少件时总利润
定为多少件时总利润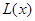 (万元)最大?并求最大值(精确到1万元).
(万元)最大?并求最大值(精确到1万元).