已知一副三角板ABE与ACD.
将两个三角板如图(5)放置,连结BD,计算∠1+∠2=___
将图(5)中的三角板BAE绕点A顺时针旋转一个锐角α

当α=_______时,AB∥CD,如图(6)并计算α+∠1+∠2=____.
‚当α=45º时,如图(7),计算α+∠1+∠2=____.
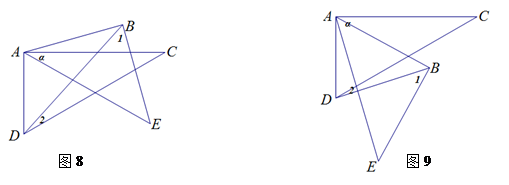
ƒ在旋转的过程中,当B点在直线CD的上方时,如图(8),α、∠1、∠2间的数量关系是否会发生变化,为什么?
„当B点运动到直线CD的下方时,如图(9)α(∠CAE)、∠1、∠2间的数量关系是否会发生变化,试说明你的结论?