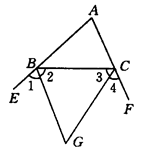
请完成下面的说明:如图①所示，△ABC的外角平分线交于G，试说明∠BGC=90°-
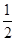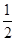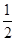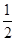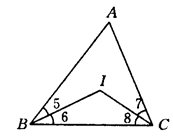
∠A． 说明：根据三角形内角和等于180°，可知∠ABC+∠ACB=180°-∠_____． 根据平角是180°，可知∠ABE+∠ACF=180°×2=360°，所以∠EBC+∠FCB=360°-（∠ABC+∠ACB）=360°-（180°-∠_____）=180°+∠______．根据角平分线的意义，可知∠2+∠3=（∠EBC+∠FCB）=（180°+∠_____）=90°+∠_______．所以∠BGC=180°-（∠2+∠3）=90°-∠____如图②所示，若△ABC的内角平分线交于点I，试说明∠BIC=90°+
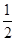∠A．用（1），（2）的结论，你能说出∠BGC和∠BIC的关系吗？（直接写出结论）
如图，在四边形ABCD中，∠DAB=∠DCB=90°，对角线AC与BD相交于点O，M、N分别是边BD、AC的中点．
（1）求证：MN⊥AC；
（2）当AC=8cm，BD=10cm时，求MN的长．
已知：如图，在△ABC中，∠C=90°，∠B=30°，AC=6，点D在边BC上，AD平分∠CAB，E为AC上的一个动点（不与A、C重合），EF⊥AB，垂足为F．
（1）求证：AD=DB；
（2）设CE=x，BF=y，求y关于x的函数解析式；
（3）当∠DEF=90°时，求BF的长？
如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，BC=6．求点D到AB边的距离．
如图，在Rt△ABC中，∠BAC=90°，AB=AC，点M、N在边BC上．
（1）如图1，如果AM=AN，求证：BM=CN；
（2）如图2，如果M、N是边BC上任意两点，并满足∠MAN=45°，那么线段BM、MN、NC是否有可能使等式MN2=BM2+NC2成立？如果成立，请证明；如果不成立，请说明理由．
如图，在等腰梯形ABCD中，AD∥BC，AC平分∠BCD，已知AD=5cm，BC=9cm，
求等腰梯形ABCD的周长．