某校为了解九年级500名学生平均每天课外阅读的时间,随机调查了该年级部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),现将有关数据整理后绘制成尚未完成的频率分布表和频数分布直方图:
| 组别 |
分组 |
频数 |
频率 |
| 1 |
14.5—24.5 |
7 |
0.14 |
| 2 |
24.5—34.5 |
a |
0.24 |
| 3 |
34.5—44.5 |
20 |
0. 4 |
| 4 |
44.5—54.5 |
6 |
b |
| 5 |
54.5—64.5 |
5 |
0.1 |

被调查的学生有 名
频率分布表中,a= ,b=
补全频数分布直方图;
被调查学生一周内平均每天课外阅读时间的中位数落在 组;
请估计该年级学生中,大约有 名学生平均每天课外阅读的时间不少于35分钟.
如图,一次函数y=kx+b与反比例函数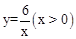 的图象交于A(m,6),B(n,3)两点.
的图象交于A(m,6),B(n,3)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出 时x的取值范围.
时x的取值范围.
(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;
(2)若(1)中的不等式的最小整数解是方程2x﹣ax=3的解,求a的值.
(1)计算: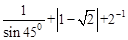 .
.
(2)先化简,再求值: ,其中
,其中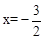 .
.
阅读材料:
(1)对于任意两个数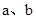 的大小比较,有下面的方法:
的大小比较,有下面的方法:
当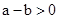 时,一定有
时,一定有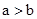 ;
;
当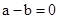 时,一定有
时,一定有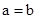 ;
;
当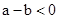 时,一定有
时,一定有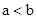 .
.
反过来也成立.因此,我们把这种比较两个数大小的方法叫做“求差法”.
(2)对于比较两个正数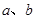 的大小时,我们还可以用它们的平方进行比较:
的大小时,我们还可以用它们的平方进行比较:
∵ ,
,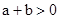
∴(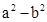 )与(
)与(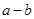 )的符号相同
)的符号相同
当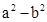 >0时,
>0时,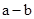 >0,得
>0,得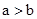
当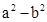 =0时,
=0时,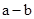 =0,得
=0,得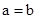
当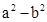 <0时,
<0时,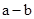 <0,得
<0,得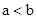
解决下列实际问题:
(1)课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸.设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为W1,李明同学的用纸总面积为W2.回答下列问题:
①W1=(用x、y的式子表示)
W2=(用x、y的式子表示)
②请你分析谁用的纸面积最大.
(2)如图1所示,要在燃气管道l上修建一个泵站,分别向A.B两镇供气,已知A.B到l的距离分别是3km、4km(即AC=3km,BE=4km),AB=xkm,现设计两种方案: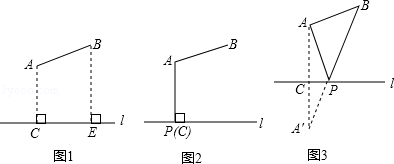
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1=km(用含x的式子表示);
②在方案二中,a2=km(用含x的式子表示);
③请你分析要使铺设的输气管道较短,应选择方案一还是方案二.
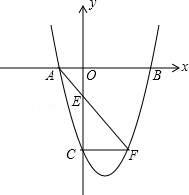
如图,抛物线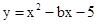 与x轴交于A.B两点(点A在点B的左侧),与y轴交于点C,点C与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
与x轴交于A.B两点(点A在点B的左侧),与y轴交于点C,点C与点F关于抛物线的对称轴对称,直线AF交y轴于点E,|OC|:|OA|=5:1.
(1)求抛物线的解析式;
(2)求直线AF的解析式;
(3)在直线AF上是否存在点P,使△CFP是直角三角形?若存在,求出P点坐标;若不存在,说明理由.