已知双曲线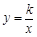 与直线
与直线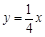 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线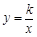 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线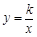 于点E,交BD于点C.
于点E,交BD于点C.若点D坐标是(-8,0),求A、B两点坐标及k的值
若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
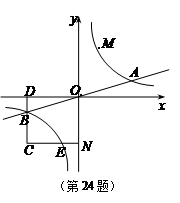
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60° ,沿山坡向上走到P处再测得点C的仰角为45° ,已知OA=100米,山坡坡度为i=1:2, 且O、A、B在同一条直线上。求电视塔OC的高度以及所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
“学生坐校车上学”的安全问题越来越受到社会的关注,某校利用周末假期,随机抽查了本校若干名学生和部分家长对“初中生坐校车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:这次抽查的家长总人数为;
请补全条形统计图和扇形统计图;
从这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率
是.
如图所示,有一个可以自由转动的圆形转盘,被平均分成四个扇形,四个扇形内
分别标有数字1、2、-3、-4.指针固定,转动转盘后任其自由停止,指针所指扇形得到相
应位置上的数字(若指针恰好指在分界线上,则该次不计,重新转动一次,直至指针落在扇
形内).若将转盘转动一次,求得到负数的概率;
若将转盘转动两次,每一次停止转动后,指针指向的扇形内的数字分别记为a、b.请你用列表法或树状图求a与 b都是方程
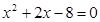 的解的概率.
的解的概率.
如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:以直线BC为对称轴作△ABC的轴对称图形,得到△
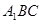 ,再将△
,再将△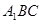 绕着点B逆时针旋转90°,得到△
绕着点B逆时针旋转90°,得到△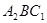 ,请依次画出△
,请依次画出△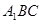 、△
、△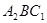 .
.求△
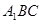 旋转至△
旋转至△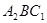 的过程中,线段
的过程中,线段 所扫过的面积(计算结果用含有π的式子表示)
所扫过的面积(计算结果用含有π的式子表示)

先化简,再求值: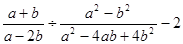 ,其中
,其中 .
.