有3张扑克牌,分别是红桃3,红桃4和黑桃5,把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张,先后两次抽得的数字分别记为S和t,求
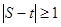 的概率
的概率甲、乙两人做游戏,现有两种方案:A方案:若两次抽得相同花色则甲胜,否则乙胜,B方案:若两次抽得数字和为奇数则甲胜,否则乙胜;请问甲选择哪种方案胜率较高?
(本题12分) 某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使
前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
(本题10分)如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.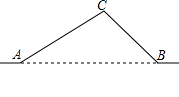
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(参考数据:sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
(本题10分)如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F ,连接OC、FC.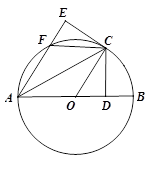
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形 AOCF是菱形.
(本题8分) 如图,在△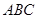 和△
和△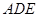 中,
中,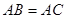 ,
,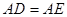 ,
,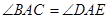 ,点
,点 在
在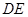 上.
上.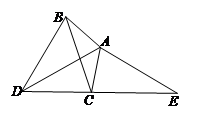
求证:(1)△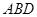 ≌△
≌△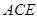 ;
;
(2) .
.
(本题8分)4张奖券中有2张是有奖的,甲、乙先后各抽一张.
(1)甲中奖的概率是;
(2)试用列树状图或列表法求甲、乙都中奖的概率.