(本题10分)如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.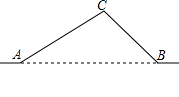
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?
(参考数据:sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
对于任意的实数x,记f(x)= .
.
例如:f(1)= =
=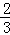 ,f(﹣2)=
,f(﹣2)= =
=
(1)计算f(2),f(-3)的值;
(2)试猜想f(x)+f(﹣x)的值,并说明理由;
(3)计算f(﹣2014)+f(﹣2013)+…+f(﹣1)+f(0)+f(1)+…+f(2013)+f(2014).
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: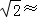 1.4,1.7)
1.4,1.7)
(1)求索道AB的长;
(2)为乙的步行速度.
如图,已知AC是⊙O的直径,PA⊥AC,连接OP,弦CB∥OP,直线PB交直线AC于点D.
(1)证明:直线PB是⊙O的切线;
(2)若BD=2PA,OA=3,PA=4,求BC的长.
今年植树节,安庆某中学组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整).
| 植树数量(棵) |
频数(人) |
频率 |
| 3 |
5 |
0.1 |
| 4 |
20 |
0.4 |
| 5 |
||
| 6 |
10 |
0.2 |
| 合计 |
50 |
1 |
(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的众数和中位数,并从描述数据集中趋势的量中选择一个恰当的量来估计该校1200名学生的植树数量.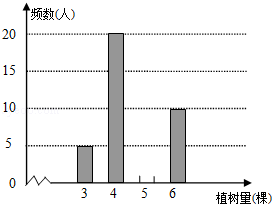
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,请按要求完成下列步骤:
(1)先将△ABC向右平移3个单位后得到△A1B1C1,再将△A1B1C1绕点B1按逆时针方向旋转90°后得到△A2B1C2;试在正方形网格中画出上述二次变换所得到的图形;
(2)求线段A1C1旋转得到A2C2的过程中,线段A1C1所扫过的面积.