某校为了解“课程选修”的情况，对报名参加“艺术鉴赏”，“科技制作”，“数学思维”，“阅读写作”这四个选修项目的学生（每人限报一项）进行抽样调查，下面是根据收集的数据绘制的不完整的统计图：
请根据图中提供的信息，解答下面的问题：
（1）此次共调查了 名学生，扇形统计图中“艺术鉴赏”部分的圆心角是 度；
（2）请把这个条形统计图补充完整；
（3）现该校共有800名学生报名参加这四个选修项目，请你估计其中有多少名学生选修“科技制作”项目.
在数轴上，A点表示2，现在点A向右移动两个单位后到达点B；再向左移动10个单位到达C点：
（1）请在数轴上表示出A点开始移动时位置及B、C点位置；
（2）当A点移动到C点时，若要再移动到原点，问必须向哪个方向移动多少个单位？
（3）请把A点从开始移动直至到达原点这一过程，用一个有理数算式表达出来.
先观察：
，
，
，
.
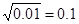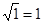（1）从题中的例子发现，当被开方数的小数点向一个方向移动2位时，算术平方根的小数点向相同方向移动位；
（2）已知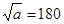
，
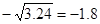，则
；
（3）已知
≈1.442，则
≈.
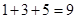
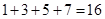
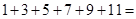
（1）第5个式子等号右边应填的数是；
（2）根据规律填空1＋3＋5＋7＋…＋(2n-1)＝；
（3）计算：1＋3＋5＋7＋…＋2013 ＝.
计算（1）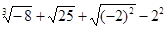
（2）
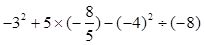
（3）
（4）
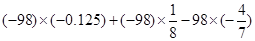
把下列各数填在相应的表示集合的大括号内：
－2 ，π，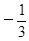
，
，
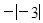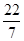，－0.3，1.7，
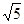，0 ， 1.1010010001……（每两个1之间依次多一个0）整数{ }
负分数{ }
无理数{ }