在不透明的口袋中,有四只形状、大小完全相同的小球,四只小球上分别标有数字1,2,3,4. 小明先从盒子里随机取出一只小球(不放回),记下数字作为平面直角坐标系内点的横坐标;再由小华随机取出一只小球,记下数字作为平面直角坐标系内点的纵坐标.用列表法或画树状图,表示所有这些点的坐标;
小刚为小明、小华两人设计了一个游戏:当上述(1)中的点在正比例函数y=2x-1图象上方时小明获胜,否则小华获胜. 你认为这个游戏公平吗?请说明理由.
将下列几何体与它的名称连接起来.
把下列各数在数轴上表示出来,再按照从小到大的顺序用“<”连接起来
0,+3.5,-3, ,-(-5)
,-(-5)
如图,已知一张长方形纸片ABCD,AB∥CD ,AD=BC=1,AB=CD=5.在长方形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.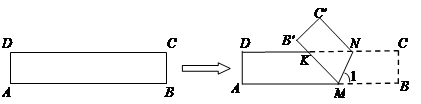
(1)请你动手操作,判断△MNK的形状一定是 ;
(2)问△MNK的面积能否小于 ?试说明理由;
?试说明理由;
(3)如何折叠能够使△MNK的面积最大?请你用备用图探究可能出现的情况,并求最大值.

如图,在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F.请解答下列问题: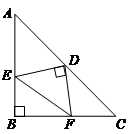
(1)连结BD,试说明∠BDE=∠CDF;
(2)求证:BE=FC;
(2)若AE=4,FC=3,求EF长.
某航船以20海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东45°处,半小时后航行到B处,此时灯塔Q与航船的距离最短.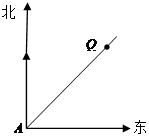
(1)请你在图中画出点B的位置;
(2)求灯塔Q到A处的距离.(精确到0.1海里)