已知函数 满足
满足 , 且对于任意
, 且对于任意 恒有
恒有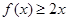 成立。
成立。
(1) 求实数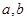 的值;
的值;
(2)设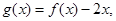 若存在实数
若存在实数 ,当
,当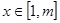 时,
时,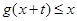 恒成立,求实数
恒成立,求实数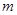 的最大值。
的最大值。
(本小题满分12分)
一个袋子中装有黄、黑两色混合在一起的豆子20公斤(两种豆子的大小相同)。现从中随机抽取50粒豆子进行发芽试验,结果如下:发芽的黄、黑两种豆子分别是27粒和16 粒,不发芽的黄、黑两种豆子分别是3粒和4粒。
粒,不发芽的黄、黑两种豆子分别是3粒和4粒。
(Ⅰ)估计黄、黑两种豆子分别有多少公斤,以及整个袋子中豆子的发芽率;
(Ⅱ)能不能有90%的把握认为发芽不发芽与豆子的颜色有关?
(Ⅲ)从3粒黄豆和2粒黑豆中任取2粒,求这2粒豆子中黑豆数X的分布列和期望。
(本小题满分12分)
在 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为 ,已知
,已知
(Ⅰ)求 的值;
的值;
(Ⅱ) 求
求 的面积
的面积
(本小题满分15分)
设函数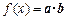 ,其中向量
,其中向量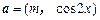 ,
,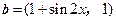 ,
,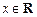 ,且
,且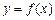 的图象经过点
的图象经过点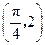 .
.
(Ⅰ)求实数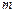 的值;
的值;
(Ⅱ)求函数 的最小值及此时
的最小值及此时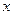 值的集合.
值的集合.
(本小题满分15分)
已知向量 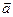 =(cos
=(cos ,sin
,sin ),
),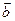 =(cos
=(cos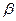 ,sin
,sin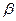 ),|
),|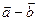 |=
|=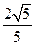 .
.
(1)求cos( -
-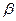 )的值;
)的值;
(2)若0< <
<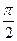 ,-
,-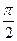 <
<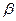 <0,且sin
<0,且sin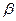 =-
=-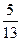 ,求sin
,求sin 的值
的值
(本小题满分14分)
已知
(1)求 ;
;
(2)若 与
与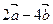 平行,求
平行,求 的值;
的值;
(3)若 与
与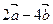 的夹角是钝角,求实数
的夹角是钝角,求实数 的取值范围.
的取值范围.