某单位在2012春节联欢会上举行一个抽奖活动:甲箱中装有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(本小题共12分)(注意:在试题卷上作答无效) 如图,四棱锥S -ABCD
如图,四棱锥S -ABCD 的底面是边长为3的正方形,SD丄底面ABCD,SB=
的底面是边长为3的正方形,SD丄底面ABCD,SB= ,点E、G分别在AB、SC上,且
,点E、G分别在AB、SC上,且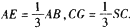
(1) 证明:BC//平面SDE;
(2) 求面SAD与面SBC所成二面角的大小.
(本小题共〖2分)(注意:在试题卷上作答无效)
某班拟从两名同学中选一人参加学校知识竞赛,现设计一个预选方案:选手从五道题中一次性随机 抽取三道进行回答,已知甲五道题中只会三道,
抽取三道进行回答,已知甲五道题中只会三道, 乙每道题答对的概率都是3/5,且每道题答对与否互不影响.
乙每道题答对的概率都是3/5,且每道题答对与否互不影响.
(1) 分别求出甲乙两人答对题数的概率分布 ;
;
(2) 你认为派谁参加比赛更合适.
(本小题共10分)(注意:在试题卷上作答无效)
斜三角形ABC的面积为S,且 ,且
,且 ,求
,求
(附加题,满分10分计入总分)已知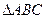 内部一点
内部一点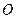 满足:
满足: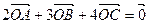 ,求:
,求: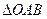 、
、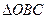 、
、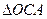 的面积的比.
的面积的比.
已知函数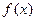 是定义在
是定义在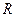 上的奇函数,当
上的奇函数,当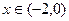 时,
时,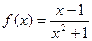 ;
;
(1)当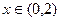 时,求
时,求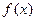 的表达式;
的表达式;
(2)在(1)的条件下,求函数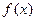 的最大值.
的最大值.