(本小题共12分)(注意:在试题卷上作答无效) 如图,四棱锥S -ABCD
如图,四棱锥S -ABCD 的底面是边长为3的正方形,SD丄底面ABCD,SB=
的底面是边长为3的正方形,SD丄底面ABCD,SB= ,点E、G分别在AB、SC上,且
,点E、G分别在AB、SC上,且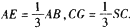
(1) 证明:BC//平面SDE;
(2) 求面SAD与面SBC所成二面角的大小.
已知向量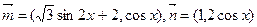 ,设函数
,设函数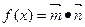 。
。
(1)求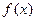 的最小正周期与单调递减区间。
的最小正周期与单调递减区间。
(2)在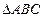 中,
中,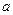 、
、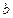 、
、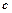 分别是角
分别是角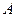 、
、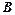 、
、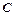
 的对边,若
的对边,若 的面积为
的面积为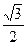 ,求
,求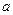 的值
的值
(本小题满分14分)
已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立。
成立。
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数 的图象有交点,若函数
的图象有交点,若函数 .
.
证明:函数 ∈
∈
(本小题满分12分)
设函数
(I)用五点法画出它在一个周期内的闭区间上的图象;
(II)求函数f(x)的最小正周期及函数f(x)的最大值
(III)求函数f(x)的单调增区间。
(本小题满分12分)已知函数 。
。
(I)判断并证明函数 的奇偶性;
的奇偶性;
(II)判断并证明函数 在
在 上的单调性;
上的单调性;
(III)求函数 在
在 上的最大和最小值。
上的最大和最小值。
(本小题满分12分)
已知角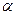 的终边与单位圆交于点P(
的终边与单位圆交于点P(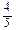 ,
, ).
).
(Ⅰ)写出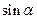 、
、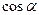 、
、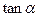 值;
值;
(Ⅱ)求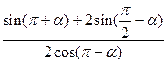 的值.
的值.