数列{an}满足a1=1,a2=2,an+2=(1+cos2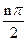 )an+sin
)an+sin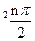 ,n=1.2.3…
,n=1.2.3…
(1)求a3.a4并求数列{an}的通项公式
(2)设bn=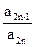 ,令 Sn=
,令 Sn=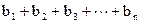 ,求 Sn
,求 Sn
已知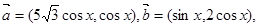 设函数
设函数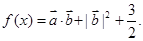 (Ⅰ)当
(Ⅰ)当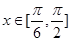 ,求函数
,求函数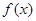 的值域;
的值域;
(Ⅱ)当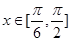 时,若
时,若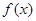 ="8," 求函数
="8," 求函数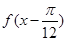 的值;
的值;
已知正项数列 中,
中,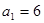 ,点
,点 在抛物线
在抛物线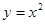 上;数列
上;数列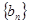 中,点
中,点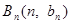 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。
(1)求数列 的通项公式;
的通项公式;
(2)若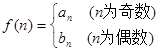 , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出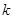 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)对任意正整数 ,不等式
,不等式 恒成立,求正数
恒成立,求正数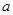 的取值范围。
的取值范围。
已知函数
(1)若存在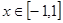 ,使得
,使得 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)解关于 的不等式
的不等式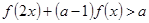 ;
;
(3)若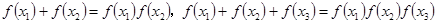 ,求
,求 的最大值.
的最大值.
某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
如图,在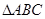 中,
中,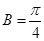 ,
, ,
,
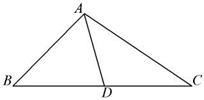
(1)求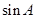 ;
;
(2)记BC的中点为D,求中线AD的长.