已知正项数列 中,
中,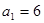 ,点
,点 在抛物线
在抛物线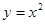 上;数列
上;数列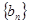 中,点
中,点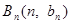 在过点(0, 1),以
在过点(0, 1),以 为斜率的直线上。
为斜率的直线上。
(1)求数列 的通项公式;
的通项公式;
(2)若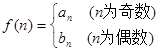 , 问是否存在
, 问是否存在 ,使
,使 成立,若存在,求出
成立,若存在,求出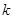 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)对任意正整数 ,不等式
,不等式 恒成立,求正数
恒成立,求正数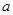 的取值范围。
的取值范围。
(本小题满分12分)已知函数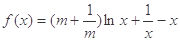 ,其中常数
,其中常数 .
.
(1)当 时,求函数
时,求函数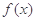 的极大值;
的极大值;
(2)当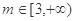 时,曲线
时,曲线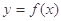 上总存在相异两点
上总存在相异两点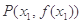 ,
,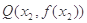 ,使得曲线
,使得曲线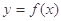 在点
在点 处的切线互相平行,求
处的切线互相平行,求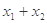 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆C的对称中心为原点O,焦点在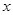 轴上,左右焦点分别为
轴上,左右焦点分别为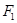 和
和 ,且
,且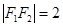 ,点
,点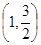 在该椭圆上.
在该椭圆上.
(1)求椭圆C的方程;
(2)过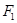 的直线
的直线 与椭圆C相交于
与椭圆C相交于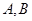 两点,若
两点,若 的面积为
的面积为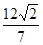 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切圆的方程.
相切圆的方程.
(本小题满分12分)如图,多面体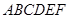 中,底面
中,底面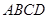 是菱形,
是菱形,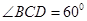 ,四边形
,四边形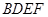 是正方形,且
是正方形,且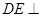 平面
平面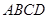 .
.
(1)求证: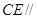 平面
平面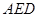 ;
;
(2)若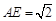 ,求多面体
,求多面体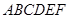 的体积
的体积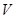 .
.
(本小题满分12分)为了了解某省各景点在大众中的熟知度,随机对15~65岁的人群抽样了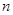 人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表.
人,回答问题“某省有哪几个著名的旅游景点?”统计结果如下图表.
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数占本组的频率 |
| 第1组 |
[15,25) |
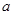 |
0.5 |
| 第2组 |
[25,35) |
18 |
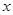 |
| 第3组 |
[35,45) |
 |
0.9 |
| 第4组 |
[45,55) |
9 |
0.36 |
| 第5组 |
[55,65] |
3 |
 |
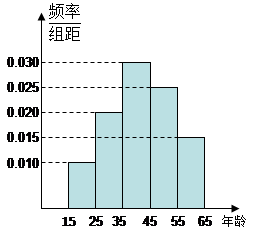
(1)分别求出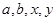 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(3)在(Ⅱ)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
(本小题满分12分)已知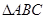 的面积为2,且满足
的面积为2,且满足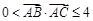 ,则
,则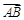 和
和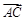 的夹角为θ.
的夹角为θ.
(1)求θ的取值范围;
(2)求函数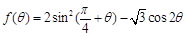 的取值范围.
的取值范围.