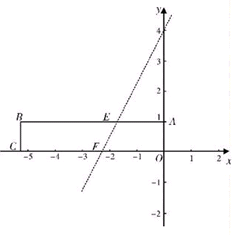
如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、
F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′求折痕所在直线EF的解析式
一抛物线经过B、E、B′三点,求此二次函数解析式;
能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
| 优等品数量(颗) |
平均数 |
方差 |
|
| A |
5.0 |
0.103 |
|
| B |
5.0 |
0.093 |
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).△AOB绕点O逆时针旋转90º后得到△A1OB1.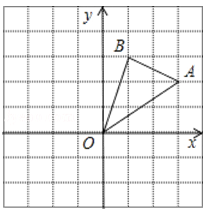
(1)在网格中画出△A1OB1,并标上字母;
(2)点A关于O点中心对称的点的坐标为 ;
(3)点A1的坐标为 ;
(4)在旋转过程中,点B经过的路径为弧BB1,那么弧BB1的长为 .
解方程:
(1)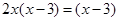
(2)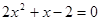
如图MN=10是⊙O的直径,AE⊥MN于E,CF⊥MN于F,AE=4,CF=3,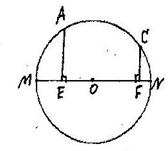
(1)在MN上找一点P,使PA+PC最短;
(2)求出PA+PC最短的距离。
为了把一个长100m宽60m的游泳池扩建成一个周长为600m的大型水上游乐场,把游泳池的长增加xm,那么x等于多少时,水上游乐场的面积为20000㎡?如果能,求出x的值;如果不能,请说明理由。