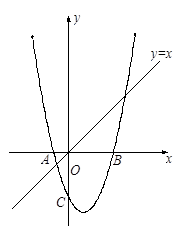如图1，已知抛物线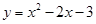
与x轴交于点A和点B，与y轴相交于点C．求A、B、C三点的坐标
点D为射线CB上的一动点（点D、B不重合），过点B作x轴的垂线BE与以点D为顶点的抛物线y＝(x－t)2＋h相交于点E，从△ADE和△ADB中任选一个三角形，求出当其面积等于△ABE的面积时的t的值；（友情提示：1、只选取一个三角形求解即可；2、若对两个三角形都作了解答，只按第一个解答给分．）
如图2，若点P是直线
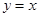上的一个动点，点Q是抛物线上的一个动点，若以点O，C，P和Q为顶点的四边形为直角梯形，求相应的点P的坐标．
互为相反数，
互为倒数，
是最小的正整数．
的值．
（2）
．
，其中
.
；
