(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为 ___ ______;
②线段AD,BE之间的数量关系为 ___ ______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D ,E在同一直线上,CM为△DCE中 DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
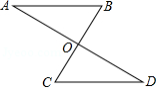
如图, , 和 相交于点 , .求证: .
如图,抛物线 的图象过点 、 、 .
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点 ,使得 的周长最小,若存在,请求出点 的坐标及 的周长;若不存在,请说明理由;
(3)在(2)的条件下,在 轴上方的抛物线上是否存在点 (不与 点重合),使得 ?若存在,请求出点 的坐标;若不存在,请说明理由.
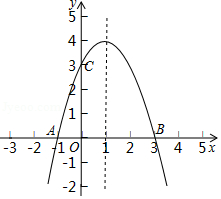
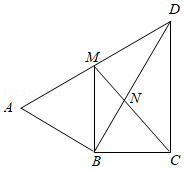
如图, , 平分 ,过点 作 交 于 .连接 交 于 .
(1)求证: ;
(2)若 , ,求 的长.
根据有理数乘法(除法)法则可知:
①若 (或 ,则 或 ;
②若 (或 ,则 或 .
根据上述知识,求不等式 的解集
解:原不等式可化为:(1) 或(2) .
由(1)得, ,
由(2)得, ,
原不等式的解集为: 或 .
请你运用所学知识,结合上述材料解答下列问题:
(1)不等式 的解集为 .
(2)求不等式 的解集(要求写出解答过程)
已知二次函数 的图象与 轴交于 , 、 , 两点,且 ,求 的值.