小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).A点所表示的实际意义是 ;= ;
求出AB所在直线的函数关系式;
如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?

某社区为了解居民对足球、篮球、排球、羽毛球和乒乓球这五种球类运动项目的喜爱情况,在社区开展了“我最喜爱的球类运动项目”的随机调查(每位被调查者必须且只能选择最喜爱的一种球类运动项目),并将调查结果进行了统计,绘制成了如图所示的两幅不完整的统计图:
(1)求本次被调查的人数;
(2)将上面的两幅统计图补充完整;
(3)若该社区喜爱这五种球类运动项目的人数大约有4000人,请你估计该社区喜爱羽毛球运动项目的人数.
如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.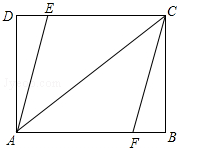
(1)若DE=BF,求证:四边形AFCE是平行四边形;
(2)若四边形AFCE是菱形,求菱形AFCE的周长.
先化简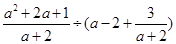 ,然后从﹣2,﹣1,1,2四个数中选择一个合适的数作为a的值代入求值.
,然后从﹣2,﹣1,1,2四个数中选择一个合适的数作为a的值代入求值.
已知抛物线C1: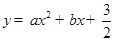 (
(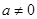 )经过点A(﹣1,0)和B(3,0).
)经过点A(﹣1,0)和B(3,0).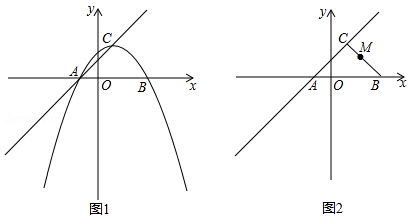
(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:
①tan∠ENM的值如何变化?请说明理由;
②点M到达点C时,直接写出点P经过的路线长.
如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD= .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE= ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若 ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.