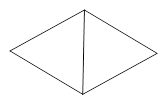
如图1是两个有一边重合的正三角形,那么由其中一个正三角形绕平面内某一点旋转后能与另一个正三角形重合,平面内可以作为旋转中心的点有_ 个.
如图2是两个有一边重合的正方形,那么由其中一个正方形绕平面内某一点旋转后能与另一个正方形重合,平面内可以作为旋转中心的点有_ 个.
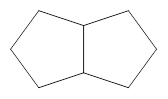
如图3是两个有一边重合的正五边形,那么由其中一个正五边形绕平面内某一点旋转后能与另一个正五边形重合,平面内可以作为旋转中心的点有_ 个.
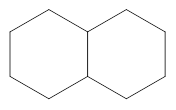
如图4是两个有一边重合的正六边形,那么由其中一个正六边形绕平面内某一点旋转后能与另一个正六边形重合,平面内可以作为旋转中心的点有_ 个.
拓展探究:两个有一边重合的正n(n≥3)边形,那么由其中一个正n边形绕平面内某一点旋转后能与另一个正n边形重合,平面内可以作为旋转中心的点有多少个?(直接写结论)
|
|

|
|