一个口袋中装有大小相同的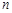 个红球(
个红球( 且
且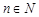 )和
)和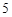 个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
个白球,一次摸奖从中摸两个球,两个球的颜色不同则为中奖。
(Ⅰ)试用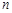 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率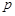 ;
;
(Ⅱ)记从口袋中三次摸奖(每次摸奖后放回)恰有一次中奖的概率为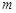 ,求
,求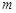 的最大值.
的最大值.
(Ⅲ)在(Ⅱ)的条件下,将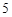 个白球全部取出后,对剩下的
个白球全部取出后,对剩下的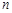 个红球全部作如下标记:记上
个红球全部作如下标记:记上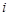 号的有
号的有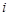 个(
个( ),其余的红球记上
),其余的红球记上 号,现从袋中任取一球。
号,现从袋中任取一球。 表示所取球的标号,求
表示所取球的标号,求 的分布列、期望和方差.
的分布列、期望和方差.
 中内角
中内角 的对边分别为
的对边分别为 ,向量
,向量 ,且
,且
(1)求锐角 的大小,
的大小,
(2)如果 ,求
,求 的面积
的面积 的最大值
的最大值
设函数f(x)="|x-1|" +|x-a|, .
.
(I)当a =4时,求不等式 的解集;
的解集;
(II)若 对
对 恒成立,求a的取值范围.
恒成立,求a的取值范围.
以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线I的参数方程为 (t为参数,O < a <
(t为参数,O < a < ),曲线C的极坐标方程为
),曲线C的极坐标方程为
(I)求曲线C的直角坐标方程;
(II)设直线l与曲线C相交于A ,B两点,当a变化时,求 的最小值.
的最小值.
如图所示,PA为 0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、
0的切线,A为切点,PBC是过点O的割线,PA ="10,PB" =5、
(I)求证: ;
;
(2)求AC的值.
已知函数 在点(1,f(1))处的切线方程为y = 2.
在点(1,f(1))处的切线方程为y = 2.
(I)求f(x)的解析式;
(II)设函数 若对任意的
若对任意的 ,总存唯一实数
,总存唯一实数 ,使得
,使得 ,求实数a的取值范围.
,求实数a的取值范围.