红星中学开展了“绿化家乡，植树造林 ”活动，并对该校的甲、乙、丙、丁四个班级种树情况进行了考察，并将收集的数据绘制了图①和图②两幅尚不完整的统计图.
请根据图中提供的信息，完成下列问题：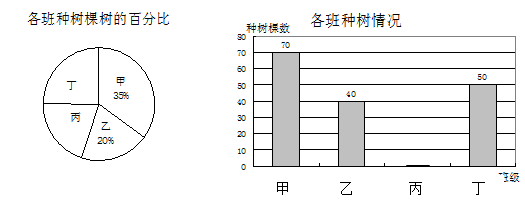
这四个班共种__▲______棵树.
请你补全两幅统计图.
若四个班种树的平均成活率是90%，全校共种树2000棵，请你估计这些树中，成活的树约有多少棵？
在平面直角坐标系中，△ABC的顶点坐标是A（-7，1），B（1，1），C（1，7）．线段DE的端点坐标是D（7，-1），E（-1，-7）．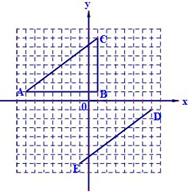
（1）试说明如何平移线段AC，使其与线段ED重合；
（2）将△ABC绕坐标原点O逆时针旋转，使AC的对应边为DE，请直接写出点B的对应点F的坐标；
（3）画出（2）中的△DEF，并和△ABC同时绕坐标原点O逆时针旋转90°，画出旋转后的图形.
如图所示，在一块长为32米，宽为15米的矩形草地上，在中间要设计一横二竖的供居民散步的小路，要使小路的面积是草地总面积的八分之一，请问小路的宽应是多少米？（注：所有小路进出口的宽度相等，且每段小路均为平行四边形）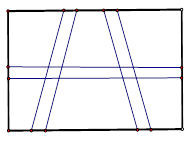
我们知道：对于任何实数
，①∵
≥0，∴+1＞0；②∵
≥0，∴+
＞0.
模仿上述方法解答：
求证：（1）对于任何实数，均有：
＞0；
（2）不论为何实数，多项式
的值总大于
的值．
某种储蓄的月利率是0.36%，今存入本金100元，求本息和（本金与利息的和）y（元）与所存月数x之间的函数关系式，并计算5个月后的本息和.
有一个周长为24的矩形场地，设矩形的一边长为x，另一边长为y（x＞y），求y与x的函数关系式，并直接写出自变量x的取值范围。