如图1，抛物线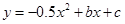
与x轴交于B(3,0) 、C(8.0)两点，抛物线另有一点A在第一象限内，连接AO、AC，且AO=AC.求抛物线的解析式；
将△OAC绕x轴旋转一周，求所得旋转体的表面积；
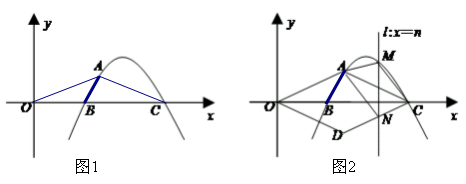
如图2，将△OAC沿x轴翻折后得△ODC，设垂直于x轴的直线l：x＝n与（1）中所求的抛物线交于点M，与CD交于点N，若直线l 沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值．
解方程组
如图，
和
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
（1）B出发时与A相距千米；
（2）B走了一段路后，自行车发生故障，进行修理，所用的时间是小时；
（3）B出发后小时与A相遇；
（4）若B的自行车不发生故障，保持出发时的速度前进，那么B几小时后与A相遇，相遇点离B的出发点多少千米？在图中标出这个相遇点C.
某一天，文具经营户花360元从文具批发市场批发了自动铅笔和钢笔共80支，到文具店去卖，自动铅笔和钢笔当天的批发价与零售价如下表所示：
| 品名 |
钢笔 |
自动铅笔 |
| 批发价（元/支） |
4.8 |
4 |
| 零售价（元/支） |
7.2 |
5.6 |
问：他卖完这些自动铅笔和钢笔可赚多少钱？
如图，点A、B在数轴上分别表示有理数
、
，在数轴上A、B两点之间的距离
．
回答下列问题：
（1）数轴上表示1和
的两点之间的距离是；(1分)
（2）数轴上表示
和的两点之间的距离表示为；(1分)
（3）若表示一个有理数，请你结合数轴求
的最小值．(2分)
请观察下列算式，找出规律并填空
=1-
， 
=-
， 
=-
，
=-
则
(1)第10个算式是= .(2分)
(2)第n个算式为=.(2分)
(3)根据以上规律解答下题：+++ … +
的值。(3分)