如图所示,轻绳一端系一质量为m的小球,另一端做成一个绳圈套在图钉A和B上,此时小球在光滑的水平平台上做半径为a、角速度为ω的匀速圆周运动。现拔掉图钉A让小球飞出,此后绳圈又被A正上方距A高为h的图钉B套住,达稳定后,小球又在平台上做匀速圆周运动。求:
(1)图钉A拔掉前,轻绳对小球的拉力大小;
(2)从拔掉图钉A到绳圈被图钉B套住前小球做什么运动?所用的时间为多少?
(3)小球最后做匀速圆周运动的角速度。
为了研究过山车的原理,物理小组提出了下列的设想:取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度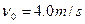 ,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道
,从某一高处水平抛出,到A点时速度方向恰沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道 的动摩擦因数
的动摩擦因数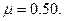 (g取10m/s2,
(g取10m/s2,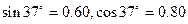 )
)
(1)要使小物块不离开轨道,并从水平轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件?
(2)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件?
(3)按照(2)的要求,小物块进入轨道后可以有多少次通过圆轨道上距水平轨道高为0.01m的某一点。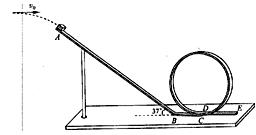
(19分) 如图所示,一个质量为 、电荷量为
、电荷量为 的正离子,在
的正离子,在 处沿图示方向以一定的速度射入磁感应强度
处沿图示方向以一定的速度射入磁感应强度 为
为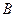 的匀强磁场中,此磁场方向是垂直纸面向里。结果离子正好从距
的匀强磁场中,此磁场方向是垂直纸面向里。结果离子正好从距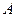 点为
点为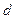 的小孔
的小孔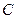 沿垂直于电场方向进入匀强电场,此电场方向与
沿垂直于电场方向进入匀强电场,此电场方向与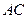 平行且向上,最后离子打在
平行且向上,最后离子打在 处,而
处,而 处距
处距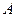 点
点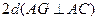 。不计离子重力,离子运动轨迹在纸面内。求:
。不计离子重力,离子运动轨迹在纸面内。求:
(1)正离子从 处运动到
处运动到 处所需时间为多少?
处所需时间为多少?
(2)正离子到达 处时的动能为多少?
处时的动能为多少?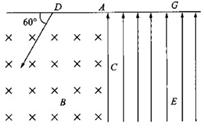
(16分) 一滑雪运动员以滑雪板和滑雪杖为工具在平直雪道上进行滑雪训练。如图所示,某次训练中,他站在雪道上第一次利用滑雪杖对雪面的作用获得水平推力F=60N而向前滑行,其作用时间为t1=1s,撤除水平推力F后经过t2=2s,他第二次利用滑雪杖对雪面的作用获得同样的水平推力且其作用时间仍为1s。已知该运动员连同装备的总质量为m=50kg,在整个运动过程中受到的滑动摩擦力大小恒为f=10N,求该运动员(可视为质点)第二次撤除水平推力后滑行的最大距离。
如图所示,固定在上、下两层水平面上的平行金属导轨 、
、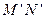 和
和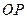 、
、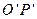 间距都是
间距都是 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道 和
和 ,两轨道间距
,两轨道间距 也均为
也均为 ,且
,且 和
和 的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的
的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的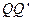 端、
端、 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端 位置,金属杆在与水平成
位置,金属杆在与水平成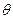 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端 位置时其速度大小
位置时其速度大小 。金属杆和导
。金属杆和导 轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
(1)已知金属杆与下层导轨间的动摩擦因数为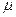 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小;
(2)金属杆运动到 位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道
位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道 和
和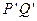 ,又在对接狭缝
,又在对接狭缝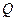 和
和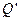 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道 和
和 的内
的内
侧,求金属杆运动到半圆轨道的最高位置 时,它对轨道作用力的大小;
时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为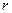 ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置 处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
如图所示,在xoy平面内,y轴左侧有一个方向竖直向下,水平宽度为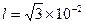 m,电场强度E=1.0×104N/C的匀强电场.在y轴右侧有一个圆心位于x轴上,半径r=0.01m的圆形磁场区域,磁场方向垂直纸面向里,磁感应强度B=0.01T,坐标为x0=0.04m处有一垂直于x轴的面积足够大的竖直荧光屏PQ.今有一束带正电的粒子从电场左侧沿+x方向射入电场,穿过电场时恰好通过坐标原点,速度大小
m,电场强度E=1.0×104N/C的匀强电场.在y轴右侧有一个圆心位于x轴上,半径r=0.01m的圆形磁场区域,磁场方向垂直纸面向里,磁感应强度B=0.01T,坐标为x0=0.04m处有一垂直于x轴的面积足够大的竖直荧光屏PQ.今有一束带正电的粒子从电场左侧沿+x方向射入电场,穿过电场时恰好通过坐标原点,速度大小 ,方向与x轴成30°角斜向下.若粒子的质量
,方向与x轴成30°角斜向下.若粒子的质量 ,电量
,电量 ,粒子的重力不计。试求:
,粒子的重力不计。试求:
(1)粒子射入电场时位置的纵坐标和初速度大小;
(2)粒子在圆形磁场中运动的最长时间;
(3)若圆形磁场可沿x轴移动,圆心O′在x轴上的移动范围为 ,由于磁场位置的不同,导致该粒子打在荧光屏上的位置也不同,试求粒子打在荧光屏上的范围。
,由于磁场位置的不同,导致该粒子打在荧光屏上的位置也不同,试求粒子打在荧光屏上的范围。