如图所示，在坐标系xoy平面内有一半径为a的 圆形区域，圆心坐标O1（a,0）圆内分布有垂直于纸面向里的匀强磁场。在直线y=a的上方和直线x=2a的左侧区域内，有一沿x轴正向的匀强电场，场强为E。在x=2a处有一平行于y轴的足够大荧光屏。在O点有一个粒子源，能在第一象限向各个方向垂直磁场发射出质量为m、电荷量为+q、速度大小为v的相同粒子。其中沿x轴正方向的一粒子，恰好能从O1点的正上方的A点射出磁场。不计粒子的重力。
（1）求磁感应强度B的大小；
（2）求所有射出的粒子打在荧光屏上的范围；
（3）若撤去荧光屏，保持电场大小不变，方向改为沿y轴负方向。求沿x轴正方向成θ=300射入磁场的粒子在电场中能到达最远的位置坐标及最后射出磁场的位置坐标。
（4）在（3）情况下，请设计一种方案能使该粒子最终从O点射出，且射出方向与初始射入O点时的方向相反，并在答题卷上画出轨迹示意图。
坐标原点O处有一点状的放射源，它向xoy平面内的x轴上方各个方向发射α粒子，α粒子的速度大小都是v0，在0<y<d的区域内分布有指向y轴正方向的匀强电场，场强大小为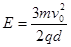
，其中q与m分别为α粒子的电量和质量；在d<y<2d的区域内分布有垂直于xoy平面的匀强磁场.ab为一块很大的平面感光板，放置于y=2d处，如图所示，.观察发现此时恰无粒子打到ab板上.（不考虑a粒子的重力）
（1）求α粒子刚进人磁场时的动能；
（2）求磁感应强度B的大小；
（3）将ab板平移到什么位置时所有粒子均能打到板上?并求出此时ab板上被α粒子打中的区域的长度.
粗糙绝缘的水平面附近存在一个平行于水平面的电场，其中某一区域的电场线与x轴平行，且沿x轴方向的电势j与坐标值x的关系如下表格所示：
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
| x/m |
0.05 |
0.10 |
0.15 |
0.20 |
0.25 |
0.30 |
0.35 |
0.40 |
0.45 |
| φ/105v |
9.00 |
4.50 |
3.00 |
2.25 |
1.80 |
1.50 |
1.29 |
1.13 |
1.00 |
根据上述表格中的数据可作出如右的j—x图像。现有一质量为0.10kg，电荷量为1.0´10-7C带正电荷的滑块（可视作质点），其与水平面的动摩擦因数为0.20。问：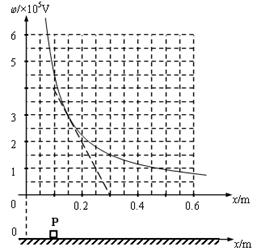
（1）由数据表格和图像给出的信息，写出沿x轴的电势j与x的函数关系表达式。
（2）若将滑块无初速地放在x=0.10m处，则滑块最终停止在何处？
（3）在上述第（2）问的整个运动过程中，它的加速度如何变化？当它位于x=0.15m时它的加速度多大？（电场中某点场强为j—x图线上某点对应的斜率）
（4）若滑块从x=0.60m处以初速度v0沿-x方向运动，要使滑块恰能回到出发点，其初速度v0应为多大？
如图所示，小球沿光滑的水平面冲上一光滑的半圆形轨道，轨道半径为R，小球在轨道的最高点对轨道压力等于小球的重力，问：
（1）小球在最高点的速度为多大？
（2）小球落地时，距最高的水平位移是多少？
（3）小球落地时速度为多大？
某人站在高60m平台边缘，以20m/s的初速度竖直向上抛出一石块，不考虑空气阻力，求：
（1）石块上升的最大高度是多少？
（2）石块从抛出到落地的时间为多少？
（3）石块落到地面时的速度大小是多少？
质量为m=3000kg的汽车在水平公路上行驶，轮胎与路面间的最大静摩擦力为15000N，汽车经过半径为r=80m的弯路时，试问：（1）如果汽车以速度v=36km/h沿弯路行驶，汽车的向心力为多大？是由什么力提供的？
（2）为保证汽车不发生侧滑，车速的最大值是多大？