甲船从A港出发顺流匀速驶向B港，乙船同时从B港出发逆流匀速驶向A港．甲船行至某处，发现船上一救生圈不知何时落入水中，立刻原路返回，找到救生圈后，继续顺流驶向B港．已知甲、乙两船在静水中的速度相同，救生圈落入水中漂流的速度和水流速度都等于1.5km/h．甲、乙两船离A港的距离y1、y2（km）与行驶时间x(h)之间的函数图象如图所示．
（1）甲船在顺流中行驶的速度为 km/h，m＝ ；
（2）①当0≤x≤4时，求y2与x之间的函数关系式；
② 甲船到达B港时，乙船离A港的距离为多少？
（3）救生圈在水中共漂流了多长时间？
小红和小慧玩纸牌游戏．如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小慧从剩余的3张牌中也抽出一张
请用树状图表示出两人抽牌可能出现的所有结果
求抽出的两张牌都是偶数的概率
如图11所示，已知抛物线
与
轴交于A、B两点，与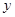
轴交于点C．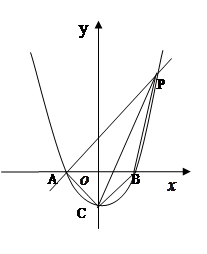
求A、B、C三点的坐标
过点A作AP∥CB交抛物线于点P，求四边形ACBP的面积．
在
轴上方的抛物线上是否存在一点M，过M作MG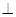
轴于点G，使以A、M、G三点为顶点的三角形与
PCA相似．若存在，请求出M点的坐标；否则，请说明理由．
如图，某小区有一长为30m，宽为20m的广场，图案如下，其中白色区域四周出口的宽度一样．小明在规定地点随意向图案内投掷小球，每球都能落在图案内，经过多次试验，发现落在黑色区域的概率是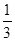
,那么白色区域四周出口的宽度应是多少？
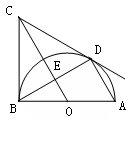
如图，AB是半圆O的直径，AD为弦，BC是半圆O的切线，OC∥AD，求证：CD是半圆O的切线
若BD＝BC＝6，求AD的长．
如图，在平面直角坐标系中，△ABC的三个顶点
坐标分别是A（2，3）、B（2，1）、C（3，2）．
①判断△ABC的形状；②如果将△ABC沿着边AC旋转，求所得旋转体的全面积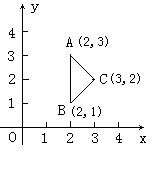
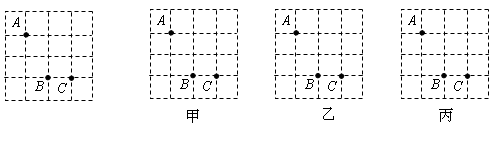
如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的格点上．
①在图甲中作出的四边形是中心对称图形但不是轴对称图形；
②在图乙中作出的四边形是轴对称图形但不是中心对称图形；
③在图丙中作出的四边形既是轴对称图形又是中心对称图形．